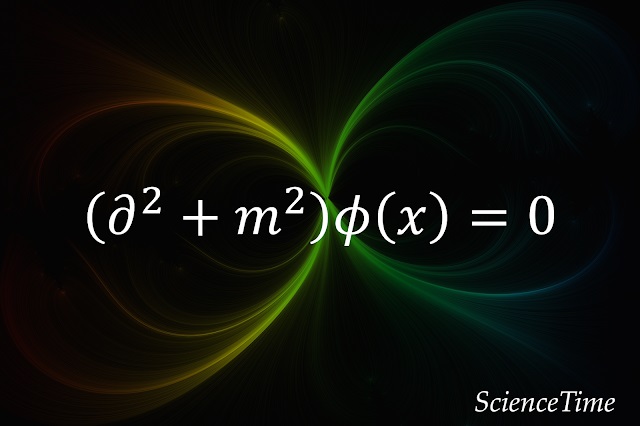Klein-Gordon方程式

はじめに

スピン0のボゾンを記述する相対論的な波動方程式Klein-Gordon方程式を導出する。まず一般的な方法での導出を行った後，Landau-Lifshitzに倣って発見的な導出法も紹介する。

注意：この記事では，$c=\hbar=1$とする自然単位系を採用し，Minkowski計量の対角成分は$(+1,-1,-1,-1)$とする。

keywords: 量子力学, 特殊相対性理論, 相対性理論, スピン, 相対論的量子力学, ボゾン

内容

一般的導出

自由粒子のSchrödinger方程式

\begin{align} i\frac{\pd}{\pd t}\psi = \frac{\nabla ^2}{2m} \psi \end{align}

は，非相対論的なエネルギーの式

\begin{align} E=\frac{\bm{p}^2}{2m} \end{align}

において，エネルギーと運動量を

\begin{align} E \to& i \frac{\pd}{\pd t} \\ \bm{p} \to & -i \nabla \end{align}

と演算子に対応付けることで得られた。

同様のことを相対論的な自由粒子のエネルギーの式

\begin{align} E^2=\bm{p}^2+m^2 \end{align}

に対して行うことで

\begin{align} \frac{\pd^2}{\pd t^2}\phi =(\nabla^2 -m^2)\phi \end{align}

が得られる。 $\pd^2=\pd_\mu \pd^\mu=\pd^2/\pd t^2 - \nabla^2$を使えば

\begin{align} \label {eq:KGeq-1} (\pd^2+m^2)\phi=0 \end{align}

と表記できる。これをKlein-Gordon方程式という。

発見的方法

続いて，Landau-Lifshitzに倣って，発見的な方法によりスピン0の自由粒子が従うべき相対的波動方程式を導出してみよう。スピン0の自由粒子の状態は，運動量$\bm{p}$のみによって指定できる。 4元運動量の並進$x_\mu \to x_\mu+\delta x_\mu$によって不変であるためには，波動関数は

\begin{align} \label {eq:plane_sol} \phi \propto e^{-ipx} \end{align}

の形であればいい。実際，並進によって波動関数の指数部分は

\begin{align} e^{-ipx} \to e^{-ipx}e^{-ip\delta x} \end{align}

となるが，位置に依存しない$\exp{(-ip\delta x)}$は不定な位相因子として無視できる。

スピン0の粒子は静止系では，3次元スカラーで記述される。これは，4次元的にはどのような形で表現されるだろうか。最も単純なのは4次元スカラー$\phi(x)$として表現することだ。しかし，例えば電磁気学におけるスカラーポテンシャルが，相対論的な枠組みでは4成分の電磁ポテンシャルベクトルの時間成分としての地位を与えられたように，今考えているスカラー関数も，4元ベクトルの時間成分として表現できるかもしれない。つまり，スピン0粒子の状態を記述する関数は

\begin{align} \phi_\mu = \left( \begin{array}{c} \phi_0 \\ \phi_1 \\ \phi_2 \\ \phi_3 \end{array} \right) \end{align}

という4元ベクトルの時間成分$\phi_0$に対応すると仮定してみる。この空間成分が静止系ですべて0になるのなら，スピン0粒子の状態が3次元スカラーで表されるという要件は満たされる。

ここで，$\phi(x)$と$\phi_\mu$を結び付ける関係式を考えてみる。自由粒子について波動方程式を構成できるのは，4元運動量演算子$\hat{p}_\mu$のみである。 $\hat{p}_\mu$を用いて作れる相対論的に不変な形の式は，左辺と右辺の添え字を揃えて

\begin{align} \label {eq:phi-phimu1} \hat{p}_\mu \phi = m \phi_\mu \end{align}

とするか，スカラー$\hat{p}^\mu \phi_\mu$を作って

\begin{align} \label {eq:phi-phimu2} \hat{p}^\mu \phi_\mu = m \phi \end{align}

としたものである。ここで定数$m$は左辺と右辺の次元を合わせるために導入されている。 1式目(\ref{eq:phi-phimu1})は，$\phi_\mu$はその時間成分$\phi_0=\phi$の勾配であることを示している。静止系では波動関数は空間成分に依存しないため，確かに$\phi_\mu$の空間成分は静止系で0となり，先の要請を満たしている。 1つ目の式(\ref{eq:phi-phimu1})の$\phi_\mu$を2つ目の式(\ref{eq:phi-phimu2})に入れると

\begin{align} \hat{p}^2\phi = m^2 \phi \end{align}

すなわち

\begin{align} \label {eq:KG1} (\hat{p}^2-m^2)\phi=0 \end{align}

が得られる。これに，平面波解(\ref{eq:plane_sol})を入れると

\begin{align} (E^2-\bm{p}^2-m^2)\phi =0 \end{align}

が与えられる。これより$m$が質量であり，(\ref{eq:KG1})は相対論的なエネルギーの式に対応することがわかる。 $\hat{p}_\mu=(i\pd_0, -i \pd_i)$より

\begin{align} \label {eq:KG} (\pd^\mu \pd_\mu + m^2) \phi=0 \end{align}

と表記できる。改めて(\ref{eq:KG1})あるいは(\ref{eq:KG})をKlein-Gordon方程式という。こうして，スピン0粒子は，波動方程式(\ref{eq:KG})を満たす4次元スカラー$\phi(x)$で表されることがわかった。

Klein-Gordon方程式

一般的導出

発見的方法

参考文献