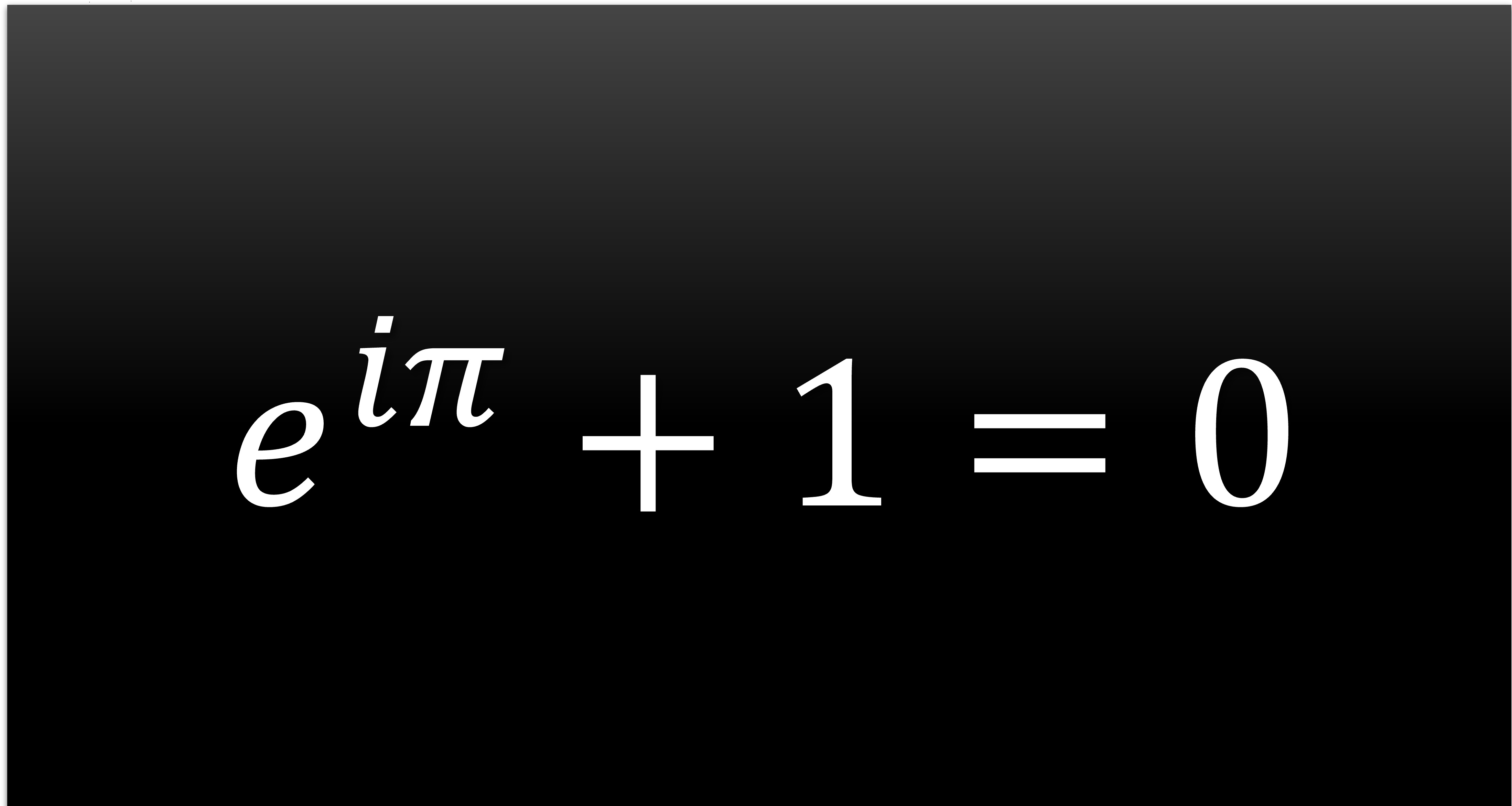Eulerの公式
Dr. SSS
2019/04/27 - 20:08:58
4788
複素解析
数学における最も素晴らしい公式…これは我々の至宝である。 ―Richard Feynman, ファインマン物理学I
はじめに
keywords: 数学, Leonhard Euler, Eulerの公式, 複素解析, Richard Feynman, 神秘
内容
ここでは，指数関数と三角関数の間に成り立つ関係式，Eulerの公式の導出を行う。 この公式は，その神秘性ゆえのポピュラリティだけでなく，物理学において極めて大きな実用的重要性も持つ。
keywords: 数学, Leonhard Euler, Eulerの公式, 複素解析, Richard Feynman, 神秘
内容
復習
まず，必要な知識をざっと示すが，より詳しくは『複素数の基礎』や『三角関数』の項を参照してもらいたい。
複素数
虚数単位$i$は，二乗して$-1$になる数
\begin{align}
i \times i = -1
\end{align}
として定義される。具体的にいくつかの累乗を考えると
\begin{align}
i^{0}=& 1, \quad i^{1}=i, \quad i^{2}=-1, \quad i^{3}=-i, \notag \\
i^{4}=& 1, \quad i^{5}=i, \quad i^{6}=-1, \quad i^{7}=-i, \cdots
\end{align}
となる。
三角関数の微分
sine関数とcosine関数の微分は
\begin{align}
(\sin x)^{\prime} &=\cos x \\
(\cos x)^{\prime} &=-\sin x
\end{align}
で与えられる。ここでプライムは$x$についての微分を表す。
Taylor展開
無限回微分可能な実関数，あるいは複素関数$f(x)$の，$x_0$周りの展開
\begin{align}
f(x)=& \sum_{k=0}^{\infty} \frac{f^{(k)}(x_0)}{k !}(x-x_0)^{k} \notag \\
=& f(x_0)+(x-x_0) f' (x_0)+\frac{(x-x_0)^{2}}{2 !} f^{\prime \prime}(x_0)+\frac{(x-x_0)^{3}}{3 !} f^{\prime \prime \prime}(x_0)+\cdots
\end{align}
をTaylor展開という。特に$x_0=0$の場合
\begin{align}
f(x)=& \sum_{k=0}^{\infty} f^{(k)}(0) \frac{x^{k}}{k !} \notag \\
=& f(0)+x f^{\prime}(0)+\frac{x^{2}}{2 !} f^{\prime \prime}(0)+\frac{x^{3}}{3 !} f^{\prime \prime \prime}(0)+\cdots
\end{align}
をMaclaurin展開と呼ぶ。
導出
指数関数のMaclaurin展開は
\begin{align}
e^z =& \sum_{k=0}^{\infty} \frac{z^{k}}{k !} \notag \\
\label {exp z}
=& 1+z+\frac{z^{2}}{2 !}+\frac{z^{3}}{3 !}+\frac{z^{4}}{4 !}+\frac{z^{5}}{5 !}+\frac{z^{6}}{6 !}+\frac{z^{7}}{7 !}\cdots
\end{align}
である。 一方$\cos x$および$\sin x$の展開はそれぞれ
\begin{align}
\cos x=& \sum_{k=0}^{\infty}(-1)^{k} \frac{x^{2 k}}{(2 k) !} \notag \\
=& 1-\frac{x^{2}}{2}+\frac{x^{4}}{4 !}-\frac{x^{6}}{6 !}+\cdots
\end{align}
および
\begin{align}
\sin x =& \sum_{k=0}^{\infty}(-1)^{k} \frac{x^{2 k+1}}{(2 k+1) !} \notag \\
=& x-\frac{x^{3}}{3 !}+\frac{x^{5}}{5 !}-\frac{x^{7}}{7 !}+\cdots
\end{align}
であるから，(\ref{exp z})で$z=ix$とすると，Eulerの公式
\begin{equation}
\begin{split}
e^{i x} &=1+i x+\frac{(i x)^{2}}{2}+\frac{(i x)^{3}}{3 !}+\frac{(i x)^{4}}{4 !}+\frac{(i x)^{5}}{5 !}+\frac{(i x)^{6}}{6 !}+\frac{(i x)^{7}}{7 !}+\cdots \\
&=1+i x-\frac{x^{2}}{2}-i \frac{x^{3}}{3 !}+\frac{x^{4}}{4 !}+i \frac{x^{5}}{5 !}-\frac{x^{6}}{6 !}-i \frac{x^{7}}{7 !}+\cdots \\
&=\left(1-\frac{x^{2}}{2}+\frac{x^{4}}{4 !}-\frac{x^{6}}{6 !}+\cdots\right)
+i\left(x-\frac{x^{3}}{3 !}+\frac{x^{5}}{5 !}-\frac{x^{7}}{7 !}+\cdots\right) \\
&=\cos x+i \sin x
\end{split}
\end{equation}
が示される。
複素平面で見ると，以下の図のようになる。
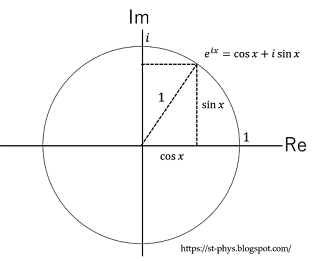
$x=\pi$を代入すると
\begin{align}
\notag
e^{i\pi} = \cos \pi +i \sin \pi
\end{align}
となり，$\cos \pi =-1$および$ \sin \pi=0$であるため，よく知れた関係式
\begin{align}
e^{i\pi} =-1
\end{align}
あるいは自明な別の表現として
\begin{align}
e^{i\pi} +1=0
\end{align}
が得られる。