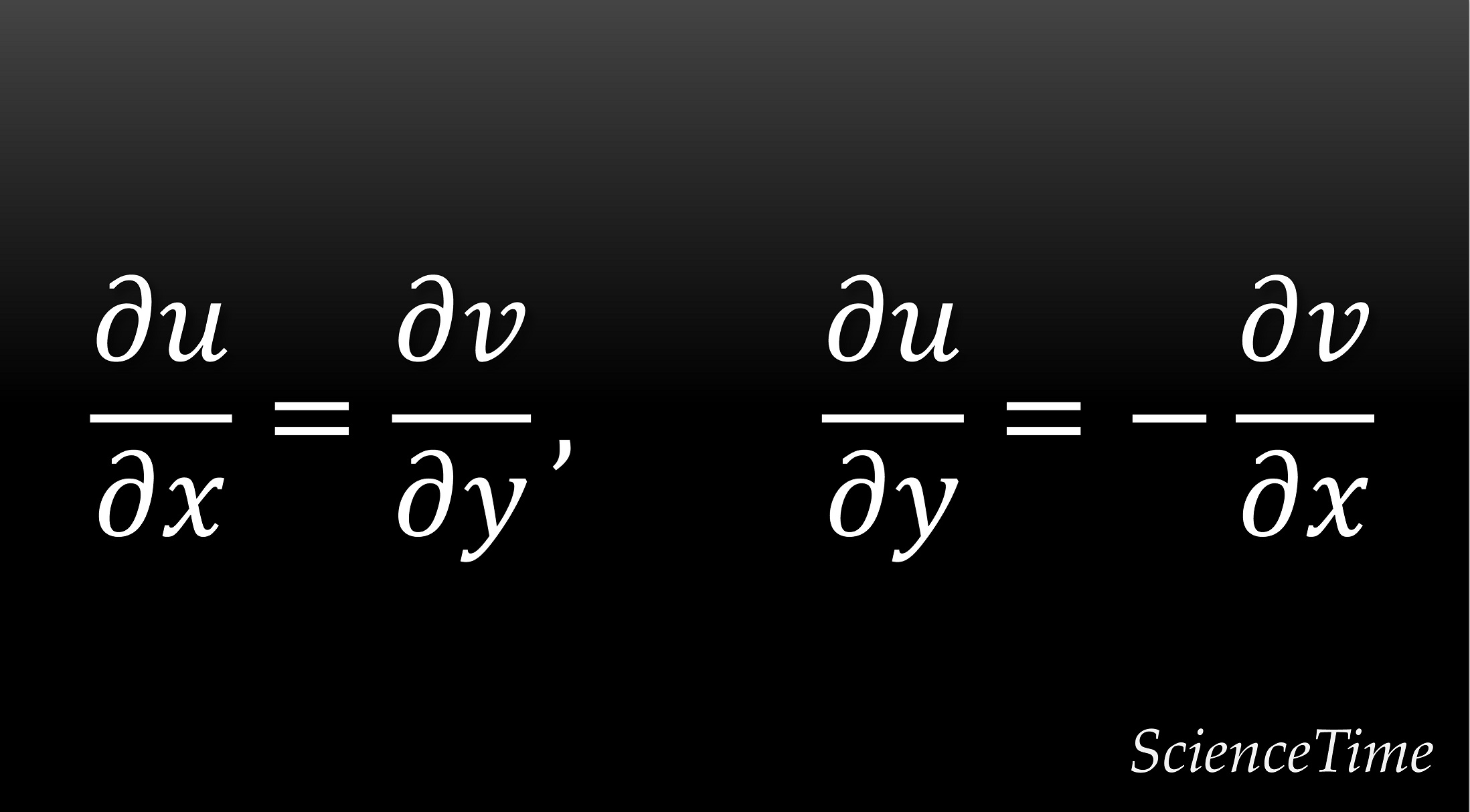複素関数の微分可能性とCauchy

Keywords:

Introduction

複素関数の微分可能性の必要十分条件を与えるCauchy–Riemann方程式について解説する。初めに実関数の微分可能性についておさらいし，後にそれとの対比で複素関数の微分可能性について説明し，最後に正則関数の定義と孤立特異点について触れる。

実関数のおさらい

実関数$f(x)$が$x=x_0$で微分可能とは

\begin{align} \label{eq:df_condition1} f'(x_0) = \lim_{x\to x_0} \frac{f(x)-f(x_0)}{x-x_0} \end{align}

が定まるということであった。これは

\begin{align} \label{eq:df_condition2} f(x) = f(x_0) + f'(x_0)\Delta x + o(\Delta x) \end{align}

と同値である。ここで$\Delta x=x-x_0$で，$o(\Delta x)$は極限操作によって消え去る部分

\begin{align} \lim_{\Delta x\to 0} \frac{|o(\Delta x)|}{|\Delta x|}\to 0 \end{align}

を表している。よって，微分可能であれば$\lim_{x\to x_0} f(x)=f(x_0)$なので$f(x)$は$x=x_0$で連続でもある。

2変数関数$f(x,y)$の場合，微分可能であるための条件(\ref{eq:df_condition2})に対応するのは

\begin{align} f(x,y) = f(x_0,y_0) +\frac{\pd f}{\pd x}\Delta x +\frac{\pd f}{\pd y}\Delta y +o(|\Delta r|) \end{align}

である。ここで$\Delta y=y-y_0$および$\Delta r=\sqrt{(\Delta x)^2+(\Delta y)^2}$である。偏微分可能であるからと言って全微分可能であるとは限らないが，$\pd f/\pd x$と$\pd f/\pd y$のどちらか一方でも連続であれば，全微分可能であると言える。

Cauchy–Riemann方程式

さて，複素数$z=x+iy$の関数$f(z)$についても同様に

\begin{align} \label{eq:dfdz} f'(z_0) = \lim_{z\to z_0} \frac{f(z)-f(z_0)}{z-z_0} \end{align}

が定まれば，$z=z_0$で微分可能であるという。あるいは条件(\ref{eq:df_condition2})に対応するのは

\begin{align} \label{eq:df_condition} f(z+\Delta z)=f(z)+f'(z)\Delta z + o(\Delta z) \end{align}

である。変数が数直線上の点に対応付けられる実関数の場合と異なるのは，$z$から$z_0$へのアプローチの仕方が無数にあることだ。つまり，複素関数$f(z)$の微分可能性の定義は，可能なすべてのアプローチの仕方に関して同じ極限値を取るという実関数の場合より厳しい要求を課している。多変数関数における偏微分も，特定の変数以外は固定して行われるため，事情は異なっている。

では，どのような関数がこの条件を満たすだろうか？それを調べるためまず，関数$f(z)$を実部と虚部に分け

\begin{align} f(z)=u(x,y)+iv(x,y) \end{align}

のように置く。以下，$f(z)$が微分可能であると仮定した場合，どのような条件が得られるかを調べる。

$z$を$\Delta z=\Delta x + i\Delta y$ずらすと，対応する$f$の増加分は

\begin{align} \Delta f = f(z+\Delta z)-f(z) = \Delta u + i \Delta v \end{align}

と表せる。対して，$f'(z)$も複素関数であるから

\begin{align} f'(z)=a+ib \end{align}

と置ける。よって(\ref{eq:df_condition})は

\begin{align} \Delta f = \Delta u + i \Delta v =& (a+ib)(\Delta x + i\Delta y) + o(\Delta z) \notag \\ =& (a\Delta x-b\Delta y) + i(b\Delta x+a\Delta y) + o(\Delta z) \end{align}

と表せる。実部と虚部がそれぞれ等式を満たさないといけないから

\begin{align} \Delta u =& a\Delta x - b\Delta y + o_R(\Delta z) \\ %%% \Delta v =& b\Delta x + a\Delta y + o_I(\Delta z) \end{align}

が成り立つ。ここで$o(\Delta z)=o_R(\Delta z)+io_I(\Delta z)$とした。これは，$u(x,y)$および$v(x,y)$がそれぞれ全微分可能であるが，それらの微分係数は独立ではなく

\begin{align} \label{eq:dfdz_ab} a=\frac{\pd u}{\pd x}=\frac{\pd v}{\pd y}, \quad b=-\frac{\pd u}{\pd y}=\frac{\pd v}{\pd x} \end{align}

のように関係づけられることを示している。言い換えれば，微分可能な複素関数は，関係式

\begin{align} \label{eq:Cauchy–Riemann_eq} \frac{\pd u}{\pd x}=\frac{\pd v}{\pd y}, \quad \frac{\pd u}{\pd y}=-\frac{\pd v}{\pd x} \end{align}

を満たす。これらの関係式をCauchy–Riemann方程式という。

上の議論では，Cauchy–Riemann方程式を満たすという条件が，関数$f(z)$が微分可能であることの必要条件であることが示されたわけであるが，次はこの条件が十分条件でもあることを示そう。 $f(z)=u(x,y)+iv(x,y)$における$u(x,y)$，$v(x,y)$がCauchy–Riemann方程式を満たすということは，$u(x,y)$，$v(x,y)$が偏導関数を持つという仮定に基づいている。偏導関数が連続であると仮定すれば

\begin{align} \Delta u =& \frac{\pd u}{\pd x}\Delta x +\frac{\pd u}{\pd y}\Delta y + o_R(\Delta z) \notag \\ %%% \Delta v =& \frac{\pd v}{\pd x}\Delta x +\frac{\pd v}{\pd y}\Delta y + o_I(\Delta z) \end{align}

と置ける。よってCauchy–Riemann方程式を用いることで

\begin{equation} \begin{split} \Delta f = \Delta u + i \Delta v =& \left( \frac{\pd u}{\pd x} + i\frac{\pd v}{\pd x} \right)\Delta x + \left( \frac{\pd u}{\pd y} + i\frac{\pd v}{\pd y} \right) \Delta y + o(\Delta z) \\ % =& \left( \frac{\pd u}{\pd x} + i\frac{\pd v}{\pd x} \right)(\Delta x+i\Delta y) + o(\Delta z) \\ % =& \left( \frac{\pd v}{\pd y} - i\frac{\pd u}{\pd y} \right)(\Delta x+i\Delta y) + o(\Delta z) \end{split} \end{equation}

となり，一意な導関数

\begin{align} f'(z) = \lim_{\Delta z\to 0} \frac{\Delta f}{\Delta z} = \left( \frac{\pd u}{\pd x} + i\frac{\pd v}{\pd x} \right) = \left( \frac{\pd v}{\pd y} - i\frac{\pd u}{\pd y} \right) \end{align}

が定まるから，$f(z)$は微分可能であると言える。この十分条件に関する議論は，あくまで$u(x,y)$，$v(x,y)$が全微分可能であるという仮定から$f(z)$の微分可能性を示していることに注意しよう。こうして次の定理を得る。

$f(z)=u(x,y)+iv(x,y)$が$z=z_0$微分可能であるための必要十分条件は，$u,v$がともに$z_0=x_0+iy_0$で微分可能であり，それらの偏微分係数がCauchy–Riemann方程式(\ref{eq:Cauchy–Riemann_eq})を満たすことである。

正則関数

上では，複素平面上の一点における微分可能性について論じた。しかし多くの場合，実用上重要になってくるのは考察の対象となる領域全体で微分可能かどうかということである。これに関係して，次の定義が与えられる

領域$D$で定義される関数$f(z)$が，$D$の各点で微分可能なとき，$f(z)$を$D$上の正則関数（regular function）という。

対して，$f(z)$が領域$\{|z-z_0|<\varepsilon\}$上の$z=z_0$を除く部分で正則である場合，$z_0$を$f(z)$の孤立特異点（isoloated singularity）という。

References

有馬朗人 and 神部勉 (1991). 物理のための数学入門複素関数論. 共立出版.

一松信 (1981). 解析学序説上・下. 裳華房.

山本直樹. (2015). 複素関数論の基礎. 裳華房.