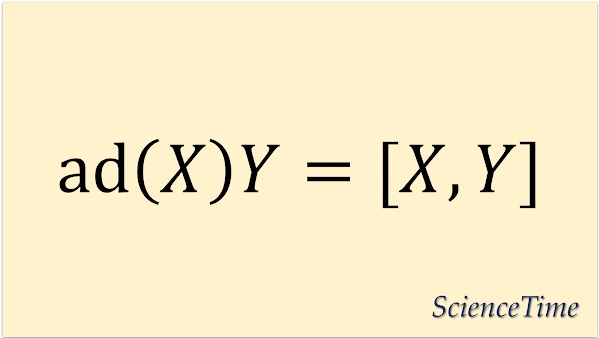Lie代数の表現：随伴表現とKilling形式

Keywords:

Introduction

Lie代数の表現と，その中で特に重要な随伴表現，および今後の議論に必要となるKilling形式について紹介する。

Lie代数とは

改めてLie代数\index[jp]{りーだいすう@Lie代数}の定義を与えておこう。 Lie代数$\frg$とは，体$F$上のベクトル空間で，かつ任意の$a,b\in F$および$x,y,z\in \frg$について，次の性質を満たす双線形演算$[x,y]\in \frg$を備えたもののことである：

\begin{equation} [ax+by,z] =a[x,z]+b[y,z] \end{equation}

\begin{equation} [x,y]=-[y,x] \end{equation}

\begin{equation} [[x,y],z] +[[y,z],x] +[[z,x],y]=0 \end{equation}

またこの演算$[,]$をLie括弧（bracket）という。

Lie代数の表現

群$G$から$GL(n,F)$への準同型写像，すなわち任意の$g_i,g_j\in G$に対して

\begin{align} \label{eq:D_homomorphic} D(g_i g_j)=D(g_i)D(g_j) \end{align}

を満たす$D$（またはそれと，それが作用するベクトル空間を合わせたもの）を，群$G$の表現というのであった。 $F$は表現空間が定義される体で，ここでは実数$R$または複素数$C$であるとする。

Lie代数の表現についても，次のように定義する。

定義： Lie代数$\frg$から$\frgl$への準同型写像$\rho$をLie代数の表現という。

Lie代数の表現が満たすべき条件を明示すると，$\forall X,\forall Y \in \frg$および$\forall a, \forall b \in F$に対し

$\rho(aX+bY)=a\rho(X)+b\rho(Y)$
$\rho([X,Y])=[\rho(X),\rho(Y)]$

である。

随伴表現

Lie代数$\mathfrak{g}$の元$X$に対し

\begin{align} \ad(X)Y=[X,Y]\in \mathfrak{g}, \ Y \in \mathfrak{g} \end{align}

を定義する。これは

\begin{align} \ad(aX+bY) = a\ \ad(X)+b\ \ad(Y) \end{align}

および

\begin{align} \ad([X,Y]) = [\ad(X),\ad(Y)] \end{align}

を満たすから，Lie代数の表現となる。これを，Lie代数の随伴表現（adjoint representation）という。

Killing形式

定義：

\begin{equation} B(X,Y)\equiv \tr(\ad(X)\ad(Y)) \end{equation}

で定義されるLie代数$\mathfrak{g}$上の双一次形式を，$\mathfrak{g}$のKilling形式（Killing form）という。

定義：すべての$X\in \frg$について$B(X,Y)=0$であるのは，$Y=0$である場合に限られるとき，Killing形式は非退化（non-degenerate）であるという。

次の定義はLie代数の分類に関するものである：

定義： Lie代数$\mathfrak{g}$のKilling形式が非退化であるとき，$\mathfrak{g}$は半単純Lie代数（semi-simple Lie algebra）であるという。

Killing形式は$\mathfrak{g}$上の計量テンソルとしての役割を果たすもので，非退化であることはこの計量テンソルの逆が定義できることを示す重要な性質である

References

Arvanitogeōrgos, A. (2003). An Introduction to Lie groups and the Geometry of Homogeneous Spaces. American Mathematical Society.

Bincer, A. M. (2013). Lie Groups and Lie Algebras: A Physicist's Perspective. Oxford University Press.

Das, A., & Okubo, S. (2014). Lie Groups and Lie Algebras for Physicists. World Scientific.

Georgi, H. (2018). Lie Algebras in Particle Physics: From Isospin to Unified Theories. CRC Press.

佐藤肇. (2000). リー代数入門: 線形代数の続編として. 裳華房.

島和久. (1981). 連続群とその表現. 岩波書店.