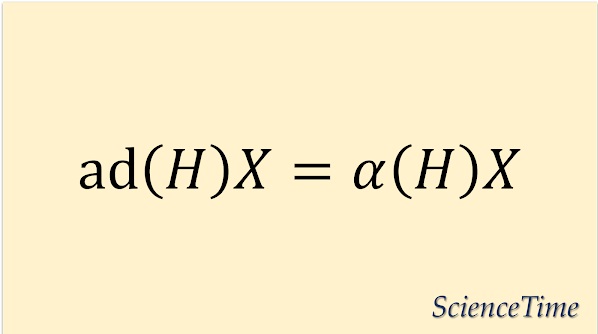内容

    1. ノート一覧
    2. 数学
    3. 群論

    Cartan部分代数とルート

    Dr. SSS 2022/06/05 - 11:42:42 3196 群論
    はじめに

    ここでは，半単純Lie代数の構造を決定す上で中心的な役割を果たすCartan部分代数とルートという概念について説明する。

    ※本ノートの内容について誤植の指摘と質問がありましたが，返信先が明記されていなかったため，こちらで内容の修正と補足をするとともに，感謝の意を示させていただきます。


    keywords: Lie群, Lie代数, 固有値, 代数学, 固有値問題, 固有ベクトル, 対角化

    Cartan部分代数

    Lie代数の可換な部分Lie代数$\frh$があり，そのすべての元と可換な$X$は，$\frh$の元にかならず含まれているとき，$\frh$は極大（maximal）であるという。 形式的に述べ直すと次のようになる：

    定義： Lie代数の可換な部分Lie代数$\frh$が極大であるとは，すべての$H\in \frh$に対し，$[X,H]=0$であれば$X\in \frh$であることをいう。

    複素半単純Lie代数$\frg$の中から，互いに可換でエルミートな元

    \begin{equation} H_i^\dagger = H_i, \quad [H_i,H_j]=0, \quad i,j=1,2,...,l \end{equation}

    を選ぶことができる。 このような元からなる部分代数のうち，次元$l$が最大のもの，すなわち極大なもの$\frh$を，Cartan部分代数（Cartan subalgebra）という。 Cartan部分代数の構成には任意性があるが，互いに同型な写像で移り合えるので，1つのLie代数に対し本質的にはただ1つのCartan部分代数が定まる。 Cartan部分代数の次元$l$をLie代数$\frg$の階数（rank）という。

    ルート

    随伴表現の性質より，各$H_i$について可換

    \begin{equation} [\ad(H_i),\ad(H_j)]=0 \end{equation}

    であるから，同時に対角化可能であり，Hermitian

    \begin{equation} \ad(H_i)^\dagger=\ad(H_i) \end{equation}

    であるから固有値は実数である。 すなわち，$l$個の実数固有値を$a_i$とし，固有値方程式

    \begin{equation} \label{eq:adX_aX} \ad(H_i)X=a_i X, \quad X\in \frg \end{equation}

    が成り立つ。

    (\ref{eq:adX_aX})において$l$個の$H_i$に対応し，$l$個の固有値$a_i$がある。 これら$a_i$は，$\frh$の双対空間$\frh^*$の元を，基底$\bm{e}^i$を用いて

    \begin{equation} \alpha =\sum_{i=1}^l a_i \bm{e}^i =a_1\bm{e}^1 +a_2\bm{e}^2+\cdots +a_l\bm{e}^l \end{equation}

    と展開した時の係数に対応する。 この$\alpha$のうち，ゼロでないものをルート（root）という。 この関係については以下で内積を導入したのちに再び議論する

    特定のルート$\alpha=\sum_i a_i\bm{e}^i$に対し(\ref{eq:adX_aX})を満たす$X\in\frg$を，$E_\alpha$と表す。 すなわち

    \begin{equation} \ad(H_i)E_\alpha=[H_i,E_\alpha]=a_i E_\alpha \end{equation}

    である。 この式を満たすために，$E_\alpha$には定数倍の任意性があることに注意しよう。 またこの式のエルミート共役は

    \begin{equation} [H_i,E_\alpha]^\dagger = -[H_i,E_\alpha^\dagger] = -\alpha E_\alpha^\dagger \end{equation}

    であるから，$\alpha$がルートであれば，$-\alpha$もルートであり

    \begin{equation} E_{-\alpha}=E_\alpha^\dagger \end{equation}

    が対応する固有ベクトルになることがわかる。

    2つのルート

    \begin{equation} \alpha=\sum_{i=1}^l a_i \bm{e}^i, \quad \beta=\sum_{i=1}^l b_i \bm{e}^i, \end{equation}

    に対し

    \begin{equation} \begin{split} \ad(H_i)[E_\alpha,E_\beta] =& [[H_i,E_\alpha],E_\beta]+[E_\alpha,[H_i,E_\beta]] \\ =& [\ad(H_i)E_\alpha,E_\beta]+[E_\alpha,\ad(H_i)E_\beta] \\ =& a_i[E_\alpha,E_\beta]+b_i[E_\alpha,E_\beta]\\ =&(a_i+b_i)[E_\alpha,E_\beta] \end{split} \end{equation}

    であるから，$\alpha=-\beta$ のとき

    \begin{equation} \ad(H_i)[E_\alpha,E_{-\alpha}]=0 \end{equation}

    となる。 $[E_\alpha,E_{-\alpha}]$はすべての$H_i$と交換する$\frg$の元であるから，すなわち$\frh$の元であり

    \begin{equation} [E_\alpha,E_{-\alpha}] =H_\alpha \equiv \sum_{i=1}^l a^i H_i, \end{equation}

    と表すことができる。

    Killing形式とCartan計量

    $\frh$と$\frh^*$，したがって$a_i$と$a^i$を関係づける計量を定義しよう。 $H_\alpha,H_i$のKilling形式を計算してみると

    \begin{equation} \begin{split} B(H_i,H_\alpha) =& \tr(\ad(H_i),\ad([E_\alpha,E_{-\alpha}])) \\ =& \tr\left(\ad(H_i) \ad(\sum_{j=1}^l a^j H_j)\right) \\ =& \tr\sum_{j=1}^la^j \left(\ad(H_i) \ad(H_j)\right) \end{split} \end{equation}

    となる。 他方，同じ量は

    \begin{equation} \begin{split} B(H_i,H_\alpha) =& \tr(\ad(H_i)[\ad(E_\alpha),\ad(E_{-\alpha})]) \\ =& \tr([\ad(H_i),\ad(E_\alpha)]\ad(E_{-\alpha})]) \\ =& \tr(\ad([H_i,E_\alpha])\ad(E_{-\alpha})]) \\ =& a_i\tr(\ad(E_\alpha)\ad(E_{-\alpha})) \end{split} \end{equation}

    でもあり，適当な規格化によって

    \begin{equation} \tr(\ad(E_\alpha)\ad(E_{-\alpha}))=1 \end{equation}

    とできるから，$H_i,H_j$のKilling形式

    \begin{equation} \label{eq:cartanMetric} g_{ij}\equiv \tr(\ad(H_i)\ad(H_j)) \end{equation}

    が計量テンソルの役割を果たし

    \begin{equation} a_i=\sum_{j=1}^l g_{ij}a^j \end{equation}

    が成り立つ。 ここで，(\ref{eq:cartanMetric})をCartan計量（Cartan metric）という。 これを用いると，$\frh$上の内積を

    \begin{equation} \alpha(H_\beta) = (\alpha,\beta) = B(H_\alpha,H_\beta) = \sum_{i,j=1}^l g_{ij} a^i b^j \end{equation}

    と定義することができる（$\frh$上でKilling形式が非退化になることについては『ルートの性質』を参照）。

    ルート（再）

    内積が定義できたので，これを利用して再び$\frh$と$\frh^*$およびルートの関係を整理しておこう。 基底$\{ H_i\}$の同時固有ベクトルを$X$とすると，(\ref{eq:adX_aX})より何らかの$H=\sum_i a^i H_i \in \frh$について

    \begin{equation} \begin{split} \ad(H)X=& \ad\left(\sum_{i=1}^l a^i H_i\right)X \\ % =& \sum_{i=1}^l a^i \ad(H_i)X \\ % =& \sum_{i=1}^l a^i a_iX \end{split} \end{equation}

    が成り立つ。 ここで$a^i$は$\frh^*$の基底$\bm{e}^i$と$H$の内積

    \begin{equation} a^i =\bm{e}^i(H) =\bm{e}^i\left(\sum_{j=1}^l a^j H_j\right) \end{equation}

    で与えられるから

    \begin{equation} \sum_{i=1}^l \bm{e}^i(H) a_i X = \alpha(H)X \end{equation}

    と書き換えられる。 したがって

    \begin{equation} \ad(H)X = \alpha(H) X \end{equation}

    である。 改めて，すべての$H$について，上の固有値方程式を成り立たせる$\alpha$のうち，ゼロでないものがルートである。

    参考文献