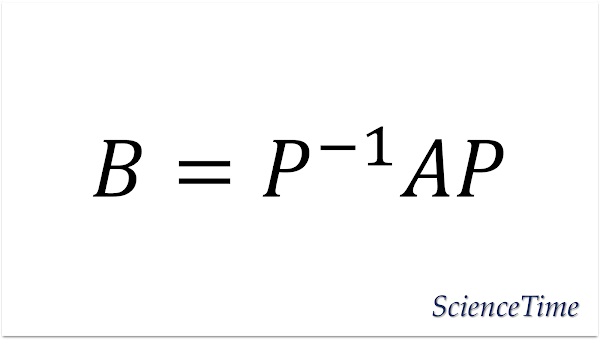行列の対角化

はじめに

ここでは，正方行列の対角化について説明する。イメージしやすいように，はじめは正方行列の次数が2の場合について説明し，それが一般化できるという議論の形をとる。

keywords: 線形代数, 行列, 固有値, 固有値問題, 対角化

内容

対角化可能であるとは

$n$次正方行列$A,B$に対し，$n$次正則行列$P$が存在し

\begin{align} \label{eq:similar} B=P^{-1}AP \end{align}

が成り立つとき，$A$と$B$は相似（similar）であるといい，正則行列によるこのような変換を，相似変換（similar transformation）という。

正方行列$A$が相似変換によって対角行列，すなわち

\begin{align} B = \left( \begin{array}{ccccc} b_{11} \\ & b_{22} & & O \\ & & \ddots & \\ & O & & \ddots & \\ & & & & b_{nn} \end{array} \right) \end{align}

の形の行列に変換できるとき，$A$は対角化可能（diagonalizable）であるという

対角化の方法と条件

$2$次の正方行列$A$に対し，それぞれ固有値$\lambda_1, \lambda_2$に属する線形独立な固有ベクトル$\bm{p}_1,\bm{p}_2$があるとする。これらを列とする行列$P=(\bm{p}_1,\bm{p}_2)$を作り，$A$を作用すると

\begin{align} AP =(A\bm{p}_1, A\bm{p}_2) =(\lambda_1\bm{p}_1, \lambda_2\bm{p}_2) =P\left( \begin{array}{cc} \lambda_1 & 0 \\ 0 & \lambda_2 \end{array} \right) \end{align}

が得られる。よって，これに，左から$P^{-1}$を作用することで

\begin{align} P^{-1}AP = \left( \begin{array}{cc} \lambda_1 & 0 \\ 0 & \lambda_2 \end{array} \right) \end{align}

と，行列$A$は対角化される。

しかし，$2$次の正方行列$A$が，2つの線形独立な固有ベクトルを持つとは限らない。例えば

\begin{align} A = \left( \begin{array}{cc} a & b \\ 0 & a \end{array} \right) \end{align}

という行列の固有方程式は

\begin{align} \Phi_A(x) = (a-x)^2=0 \end{align}

であるから，固有値は重複度2を持つ1つのみで，対応する固有ベクトルは$c\bm{e}_1$（$c$は0でない定数）という形のものに限られる。すると$P$は

\begin{align} P = \left( \begin{array}{cc} c_1 & c_2 \\ 0 & 0 \end{array} \right) \end{align}

という形のものに限られ，正則でない（逆行列を持たない）ため，上の対角化の手続きを行うことができない。

異なる固有値に属する固有ベクトルは線形独立であるため問題ないが，重複度が2以上の固有値がある場合に$A$が対角化可能であるためには，重複する固有値に対応する固有ベクトルが線形独立になっていないといけないということである。

これらの議論は，任意の次数に一般化出来て，次のことが言える：

定理： $n$次正方行列$A$は，$n$個の線形独立な固有ベクトルを持つとき，対角化可能である。

同時固有ベクトルと同時対角化

定理： $n$次正方行列$A,B$が可換なら（$AB=BA$なら），同時に両者の固有ベクトルとなるベクトル，すなわち$\lambda,\mu \in C$に対し

\begin{align} A\bm{x}=\lambda \bm{x}, \ B\bm{x}=\mu \bm{x} \end{align}

となるベクトル$\bm{x}$が存在する。このようなベクトルを，$A,B$の同時固有ベクトル（common eigenvector）という。

実際，$\bm{x}$を$n$次正方行列$A,B$の同時固有ベクトル，$\lambda,\mu$をそれぞれの固有値とすると

\begin{align} B(A\bm{x}) =& B(\lambda \bm{x}) = \mu \lambda \bm{x} \notag \\ A(B\bm{x}) =& A(\mu \bm{x}) = \mu \lambda \bm{x} \end{align}

となるから

\begin{align} (AB-BA)\bm{x}=0 \end{align}

が成り立つ。よって，もし$A,B$の固有値に縮退がなく，$n$個の線形独立な固有ベクトルの組を共有していれば，$A,B$は可換である。反対に，$A,B$が可換なら

\begin{align} A(B\bm{x})=B(A\bm{x})=\lambda(B\bm{x}) \end{align}

より，$B\bm{x}$も固有値$\lambda$に対応する$A$の固有ベクトルとなる。固有ベクトルに縮退がなければ$B\bm{x}$も$\bm{x}$に比例しないといけないから，$\bm{x}$は$B$の固有ベクトルでもある。

この性質は固有値に縮退がある場合にも成り立つ。そしてこのことから，次のことが言える：

定理： $n$次正方行列$A,B$がともに対角化可能で，互いに可換であるなら，それらは同時対角化可能（simultaneously diagonalizable）である。すなわち

\begin{align} P^{-1}AP, \ P^{-1}BP \end{align}

がともに対角行列であるような$n$次正方行列$P$が存在する。

行列の対角化

対角化可能であるとは

対角化の方法と条件

同時固有ベクトルと同時対角化

参考文献