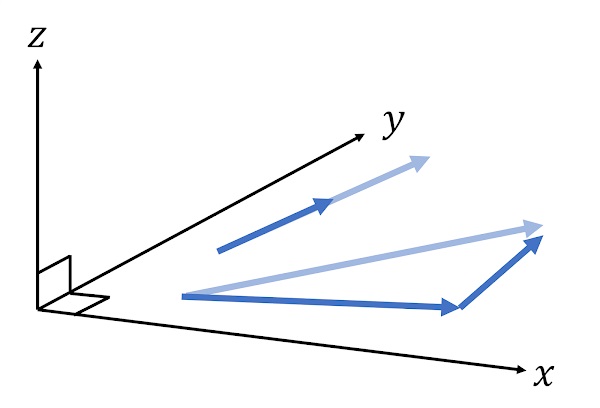
ベクトル空間とは

はじめに

初等的な物理の範囲では，ベクトルとは大きさと向きを持った量で，矢印で表現できるようなものだと習う。例えば2次元平面上の矢印としてのベクトルを考えると，これらのベクトルを定数倍して長さを変えたり，足し合わせたりした結果，その平面から飛び出たベクトルが出来上がるということはなく，得られたベクトルもまた同じ平面内に含まれる（トップの図を参照）。

線形代数では，こうしたベクトルの持つ性質を抽出して，より一般的な集合についても適用可能なものとしてベクトル空間という概念を定義する。具体的には，たとえそれがどんなに抽象的な集合で，幾何学的なイメージを当てはめることが困難なものであっても，任意の元について，定数倍したり元同士を足し合わせたりした結果得られるものが，また元の集合に含まれるものと一致するならば，その集合はベクトル空間とみなされ，その集合の元はベクトルと呼ばれる。

以下では，いま述べたことをより形式的な形で記述しなおし，関連する基本概念を説明する。

keywords: 線形代数, 体, 代数学, ベクトル空間

内容

ベクトル空間の定義

形式的には，ベクトル空間は以下のように定義される。

定義：

集合$V$がベクトル空間（vector space）あるいは線形空間（linear space）であるとは， $V$の任意の2元$\bm{u},\bm{v}$について

$\bm{u}+\bm{v} \in V$ （和）
$a\bm{v} \in V$ （スカラー倍）

が定められ，任意の$\bm{u},\bm{v},\bm{w}\in V$と$a,b \in R$について以下の性質が成り立つことをいう：

$(\bm{u}+\bm{v})+\bm{w}=\bm{u}+(\bm{v}+\bm{w})$ （結合法則）
$\bm{u}+\bm{v}=\bm{v}+\bm{u}$ （交換法則）
$\bm{o}+\bm{v}=\bm{v}$が成り立つゼロベクトル$\bm{o} \in V$が存在する。
$\bm{v}+\bm{v}'=\bm{o}$となる$\bm{v}'\in V$が存在する（このとき$\bm{v}'$を$-\bm{v}$と書き，$\bm{v}$の逆ベクトルという）。
$(a+b)\bm{v}=a\bm{v}+b\bm{v}$
$a(\bm{u}+\bm{v})=a\bm{u}+a\bm{v}$
$(ab)\bm{v}=a(b\bm{v})$
$1\bm{v}=\bm{v}$

このとき，$V$の元をベクトル（vector），$R$の元をスカラー（scalar）という。

つまり，ざっくり言えば，ベクトル空間とは和と定数倍が定義された集合のことである。

上では，スカラーを実数の集合$R$の元であるとしたが，代わりに例えば複素数の集合$C$の元として定義することもできる。ベクトル空間$V$のスカラーを実数とすることを明示する場合は，$V$を$R$上のベクトル空間，あるいは実ベクトル空間という。他方，複素数とすることを明示する場合は$C$上のベクトル空間，あるいは複素ベクトル空間という。さらに，スカラーは一般に四則演算ができる任意の集合$F$（それを体（field）という）の元として定義することができ，これに応じて，$V$を体$F$上のベクトル空間という。

線形結合

ベクトル$\bm{v}_1,\bm{v}_2,...,\bm{v}_k$をスカラー倍して加えた

\begin{align} a_1\bm{v}_1+a_2\bm{v}_2+...+a_k\bm{v}_k \end{align}

を，$\bm{v}_1,\bm{v}_2,...,\bm{v}_k$の1次結合，あるいは線形結合（linear combination）という。

ベクトル$\bm{u}$と$\bm{v}$について，$a=b=0$でない係数$a,b$を適切に選ぶことで

\begin{align} \label {eq:au+bv} a\bm{u}+b\bm{v}=\bm{o} \end{align}

とできるとき，$\bm{u}$と$\bm{v}$は互いに，線形従属（linearly dependent）であるという。他方，係数$a,b$を$a=b=0$とする以外にどう選んでも(\ref{eq:au+bv})のようにできないとき，$\bm{u}$と$\bm{v}$は互いに，線形独立（linearly independent）であるという。

2つのベクトルの場合に限らず，一般に，$a_1=a_2=...=a_k=0$のときを除いて

\begin{align} a_1\bm{v}_1+a_2\bm{v}_2+...+a_k\bm{v}_k=\bm{o} \end{align}

とならないとき，$\bm{v}_1,\bm{v}_2,...,\bm{v}_k$は線形独立，そうでない場合を，線形従属であるという。

ベクトル空間の基底

ベクトル空間$V$の元の組$\bm{u}_1,...,\bm{u}_k$が線形独立で，かつ$V$の任意の元をこれらの線形結合で表せるとき，$\bm{u}_1,...,\bm{u}_k$からなる$V$の部分集合$B$を$V$の基底（basis）という。そして，あるベクトル$\bm{v}$を，基底を用いて

\begin{align} \bm{v}= a_1 \bm{u}_1 + a_2 \bm{u}_2 + ... + a_k \bm{u}_k \end{align}

と表したとき，$a_1,...,a_k$を$B$に関する$\bm{v}$座標といい，$a_i$をベクトル$\bm{v}$の$i$成分と呼ぶ。

基底の取り方は一意ではないが，基底を構成するベクトルの数は基底の選び方に依らない。ベクトル空間$V$に有限個の元からなる基底が存在するとき，ベクトル空間$V$は有限次元であるといい，基底の元の個数をそのベクトル空間の次元（dimension）という。有限個の基底が存在しない場合，そのベクトル空間は無限次元であるという。

例えば数ベクトル空間$R^n$において

\begin{equation} \begin{split} \bm{e}_1=&(1,0,...,0), \\ \bm{e}_2=&(0,1,...,0), \\ \vdots \\ \bm{e}_n=&(0,0,...,1) \end{split} \end{equation}

は，$R^n$の基底となる。このように，$i$番目の成分のみが$1$で，残りはすべて$0$である$R^n$の基底$\{\bm{e}_i\}$を，$R^n$の標準基底（standard basis）という。

ベクトル空間とは

ベクトル空間の定義

線形結合

ベクトル空間の基底

参考文献