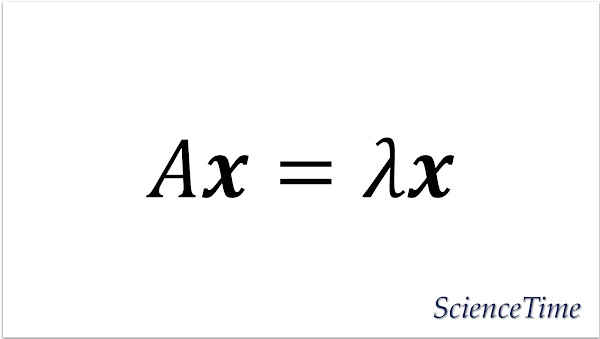固有値と固有方程式

Keywords:

固有ベクトル線形代数固有値固有値問題

Introduction

ここでは，線形変換の固有値と固有ベクトルおよびそれらと関係するいくつかの概念について説明する。

固有値と固有ベクトル

正方行列$A$と，$\bm{0}$でないベクトル$\bm{x}$，そしてある数$\lambda$に対し

\begin{equation} \label{eq:eign_eq} A\bm{x}=\lambda \bm{x} \end{equation}

が成り立つとき，$\lambda$を$A$の固有値（eigenvalue），$\bm{x}$を固有値$\lambda$に属する（対応する）固有ベクトル（eigenvector）という。

与えられた正方行列$A$の固有値を求める問題を，固有値問題（eigenvalue problem）という。式(\ref{eq:eign_eq})は，単位行列$I$を用いて

\begin{align} \label{eq:eigen_prob} (A-\lambda I)\bm{x}=0 \end{align}

と書き換えられる。

\begin{align} A\bm{x}=\bm{0} \end{align}

を満たす$\bm{x}$の集合

\begin{align} \ker(A)=\{\bm{x} \ | \ A\bm{x}=\bm{0} \} \end{align}

を$A$の核（karnel）というが，固有ベクトルとは$\ker(A-\lambda I)$に属する$\bm{0}$以外のベクトルということもできる。

もし(\ref{eq:eigen_prob})の左辺の行列$(A-\lambda I)$に逆行列が存在すれば，それを左からかけることで$\bm{x}=\bm{0}$となってしまうから，これが$\bm{x}=\bm{0}$でない非自明な解を持つためには，$(A-\lambda I)$に逆行列が存在しないこと，すなわち$\det(A-\lambda I)=0$であることが必要条件となる。

定理： $A$の異なる固有値に属する固有ベクトルは，線形独立である。

proof

固有値$\lambda_1,...,\lambda_m$に属するゼロでない固有ベクトルを$\bm{x}_1,...,\bm{x}_m$とする。
これら固有ベクトルが線形独立でないとすると，$\bm{x}_1$から$\bm{x}_i$までは線形独立だが，$\bm{x}_{1},...,\bm{x}_{i+1}$は線形従属であるという番号$i$がどこかにあるはずである。
すると，$\bm{x}_1$から$\bm{x}_i$となんらかの数$c_1,...,c_i$を組み合わせることで
\begin{align} \label{eq:xi+1} \bm{x}_{i+1} = c_1 \bm{x}_1+...+c_i\bm{x}_i \end{align}
という関係式を作ることができる。
これに$A$を作用すると
\begin{align} \lambda_{i+1}\bm{x}_{i+1} = c_1 \lambda_1 \bm{x}_1+...+c_i \lambda_i \bm{x}_i \end{align}
および
\begin{align} \lambda_{i+1}\bm{x}_{i+1} = \lambda_{i+1}(c_1 \bm{x}_1+...+c_i\bm{x}_i) \end{align}
という2通りの式が作れ，これらの差を取ることで
\begin{align} \bm{0}= c_1 (\lambda_1-\lambda_{i+1}) \bm{x}_1+... +c_i (\lambda_i-\lambda_{i+1}) \bm{x}_i \end{align}
が得られる。
$\bm{x}_1$から$\bm{x}_i$は線形独立で，固有値はすべて異なるものであるという仮定であるから，上の式が恒等的に成り立つには$c_j=0 \ (j=1,...,i)$でないといけない。すると一方(\ref{eq:xi+1})より，$\bm{x}_{i+1}=\bm{0}$ということになってしまうが，これも$\bm{x}_{i+1}$がゼロでない固有ベクトルであるという仮定に反する。
よって$\bm{x}_1,...,\bm{x}_m$は線形従属ではありえない。すなわち線形独立である。

□

固有方程式

$A$の次数を$n$とし，$A$の成分を$a_{ij}, (i,j=1,...,n)$とすると，上で述べた(\ref{eq:eign_eq})が$\bm{x}=\bm{0}$でない解を持つための条件は

\begin{align} \Phi_A(\lambda) \equiv \det(A-\lambda I)= \left| \begin{array}{cccc} a_{11}-\lambda & a_{12} & ...& a_{1n} \\ a_{21} & a_{22}-\lambda &... & a_{2n} \\ \vdots & \ddots & \vdots & \vdots \\ a_{n1} & a_{n2} & ... & a_{nn}-\lambda \end{array} \right|=0 \end{align}

と表せる。

この式の左辺は$\lambda$についての$n$次の多項式

\begin{align} \label{eq:chara_poly} \Phi_A(\lambda) = c_n \lambda^n+c_{n-1} \lambda^{n-1}+...+c_1\lambda+ c_0 \end{align}

であるから，重根を含めて$n$個の根を持つ。多項式(\ref{eq:chara_poly})を，$A$の固有多項式（characteristic polynomial）（または特性多項式）という。また，$\Phi_A(\lambda)=0$を固有方程式（characteristic equation）または永年方程式（secular equation）という。

固有方程式に重解があるとき，その固有値は縮退している（degenerate）という。

Cayley-Hamiltonの定理

固有値多項式に関する1つの重要な定理を紹介する。

2次の正方行列$A$の成分を$a_{ij}, (i,j=1,2)$と表すと，$A$の固有値多項式は

\begin{align} \Phi_A(x) =& \det \left( \begin{array}{cc} a_{11}-x & a_{12} \\ a_{21} & a_{22}-x \end{array} \right) \notag \\ =& x^2-(a_{11}+a_{22})x +a_{11}a_{22}-a_{12}a_{21} \end{align}

となる。この$x$を行列$A$自身で取り換えてみると

\begin{align} \Phi_A(A) =& A^2-(a_{11}+a_{22})A +(a_{11}a_{22}-a_{12}a_{21})I \notag \\ =& \left( \begin{array}{cc} a_{11}^2+a_{12}a_{21} & a_{11}a_{12}+a_{12}a_{22} \\ a_{21}a_{11}+a_{22}a_{21} & a_{21}a_{12}+a_{22}^2 \end{array} \right) \notag \\ &- \left( \begin{array}{cc} a_{11}^2+a_{11}a_{22} & a_{11}a_{12}+a_{12}a_{22} \\ a_{21}a_{11}+a_{22}a_{21} & a_{11}a_{22}+a_{22}^2 \end{array} \right) \notag \\ &+ \left( \begin{array}{cc} a_{11}a_{22}-a_{12}a_{21} & 0 \\ 0 & a_{11}a_{22}-a_{12}a_{21} \end{array} \right) \notag \\ =& O \end{align}

が得られる（$O$はゼロ行列）。 $A$の成分について具体的な仮定は何もしていないので，これは任意の2次の正方行列について成り立つ。そして，この関係は任意の次数について成り立つことがわかっている。

すなわち

定理（Cayley-Hamiltonの定理）： $n$次の正方行列$A$の固有多項式

\begin{align} \Phi_A(x)=\sum_{i=0}^n c_i x^{i} \end{align}

において

\begin{align} \Phi_A(A)=O \end{align}

が成り立つ（$O$はゼロ行列）。

References

長谷川浩司. (2004). 線型代数［改訂版］. 日本評論社

中原幹夫. (2016). 量子物理学のための線形代数―ベクトルから量子情報へ. 培風館.

志賀浩二. (1991). 固有値問題30講 (数学30講シリーズ). 朝倉書店