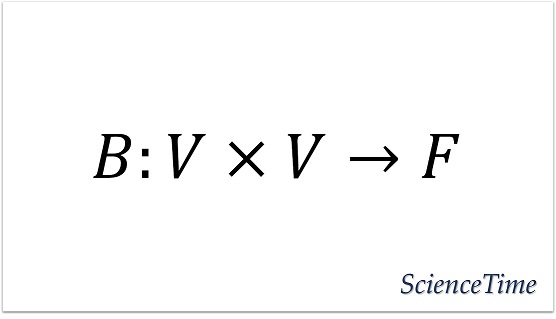線形代数とベクトル解析 2021-05-30

双一次形式

ScienceTime Team
296 views
双一次形式
Keywords:
線形代数 内積 ベクトル空間

Introduction

双一次形式とは，2つのベクトルからスカラー（実数，複素数，四元数など）を与える双線形な（それぞれの引数に対して線形な）関数のことである。 最も身近な例が，Euclid空間上の内積である。 以下で，これについてより形式的な定義と，いくつかの性質についての説明を与える。

双一次形式の定義

定義： 双一次形式（bilinear form）［または双線形形式］とは，$U,V$を体$F$上のベクトル空間としたとき，$U\times V$から$F$への写像で，次の条件を満たすものである：

\begin{align} \notag B(ax+bx',y)=&aB(x,y)+bB(x',y) \\ \notag B(x,ay+by')=&aB(x,y)+bB(x,y') \end{align}

ここで，$x,x' \in U, y,y' \in V$である。

双一次形式$B$は，任意の$x,y$について$B(x,y)=B(y,x)$であるとき対称（symmetric），$B(x,y)=-B(x,y)$であるとき反対称（anti-symmetric）または歪対称（skew-symmetric），$B(x,x)=0$であるときシンプレクティック（symplectic）であるという。

行列表現

以下，$U=V$の場合に限って考える。 $V$の次元を$n$とし，その基底を$\{ \bm{e}_i \}_{i=1}^n$とすると，双一次形式は行列

\begin{align} B_{ij}=B(\bm{e}_i,\bm{e}_j) \end{align}

によって一意に決定できる。 実際$x=\sum_i x^i \bm{e}_i$，$y=\sum_j y^j \bm{e}_j$とすると

\begin{align} B(x,y) = \sum_{ij} B(x^i\bm{e}_i,y^j\bm{e}_j) = \sum_{ij} B_{ij}x^iy^j \end{align}

である。

非退化性

$x,y \in V$に対し

\begin{align} B_y(x)=B(x,y) \end{align}

とすれば，$B_y$は$V$上の線形関数となる。 任意の$y\in V$に対して$B(x,y)=0$なら，$x=0$であるとき，$B$は 非退化（non-degenerate）であるという。

非退化である場合，任意の$y\in V$について$B_x(y)=B(x,y)=0$なら，$x=0$ということであるが，これは，任意の$y$に対して

\begin{equation} B(x-x',y) =B_{x-x'}(y) =0 \end{equation}

であれば

\begin{equation} \label{eq:bilinear_x-x'} x-x'=0 \end{equation}

であることを意味している。 他方，上の条件は線形性より

\begin{equation} \label{eq:bilinear_Bx-Bx'} B(x-x',y) =B_x(y)-B_{x'}(y)=0 \end{equation}

でもあるから，このことは，写像$\varphi: V\to V^*,\ x\to B_x$が単射であることを意味している。 また，その逆も成り立つ。 なぜなら，$x$と$B_x$の対応関係が一対一でなければ，(\ref{eq:bilinear_x-x'})と(\ref{eq:bilinear_Bx-Bx'})の対応関係が保証されなくなるためである。 したがって，$V$と$V^*$の元は一対一に対応付けられる（$V$と$V^*$は同型である）。 よって

定理： 双線形関数$B$が非退化であるためには，写像$\varphi: V\to V^*,\ x\to B_x$が同型写像であることが必要十分条件である。

Euclid内積

上で導入した概念を用いて，実Euclid空間$R^n$における内積の定義を与えよう。 Euclid空間$R^n$上の内積とは，任意の2つの数ベクトル$\bm{x}=(x^1,...,x^n)$と$\bm{y}=(y^1,...,y^n)$を，実数に対応付ける非退化な関数

\begin{align} \langle \bm{x},\bm{y} \rangle = x^i y^i \end{align}

のことであり，以下のいくつかの性質を満たす。

まず，対称性

\begin{align} \langle\bm{x},\bm{y}\rangle = \langle\bm{y},\bm{x}\rangle \end{align}

および双線形性

\begin{align} \langle a\bm{x}+b\bm{x}',\bm{y}\rangle = & a\langle\bm{x},\bm{y}\rangle + b\langle\bm{x}',\bm{y}\rangle \\ % \langle \bm{x},a\bm{y}+b\bm{y}' \rangle = & a\langle\bm{x},\bm{y}\rangle + b\langle\bm{x},\bm{y}' \rangle \end{align}

である。

さらに，同一のベクトル同士の内積について

\begin{align} \langle\bm{x},\bm{x}\rangle \geq 0 \end{align}

であり，等式が成り立つときは$\bm{x}=0$に限られる。 $\bm{x}=0$でない場合，必ず正の値を取ることを正定値性（positive definiteness）という。

これらをまとめると，実Euclid空間における内積とは，「非退化で正定値かつ対称な双線形関数のこと」であるといえる。


References

  • 佐武 一郎. (1974). 線型代数学(増補版). 裳華房.
  • Schutz, B. F. (1980). Geometrical methods of mathematical physics. Cambridge university press.
    ――(1987). 物理学における幾何学的方法. 家正則 他 訳. 物理学叢書
  • 志賀 浩二. (1989). ベクトル解析30講. 朝倉書店.
  • Szekeres, P. (2004). A course in modern mathematical physics: groups, Hilbert space and differential geometry. Cambridge University Press.