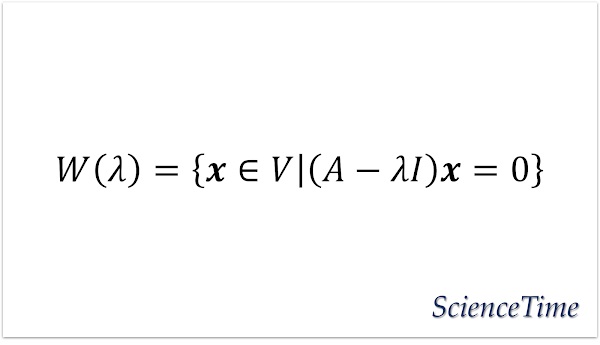固有空間と固有空間分解
Dr. SSS
2021/06/23 - 11:36:05
4650
線形代数とベクトル解析
固有空間
$V$を$C$上のベクトル空間，$A$を$V$の線形変換とする。 $A$の固有値$\lambda$に対して定義される$V$の部分空間
\begin{align}
W(\lambda)\equiv \{ \bm{x}\in V \ | \ (A-\lambda I) \bm{x}=0 \}
\end{align}
を，固有値$\lambda$に属する（対応する）固有空間（eigenspace）という。 同じものを$W_\lambda$のようにも記す。
ベクトル空間$V$の部分空間$W$が
\begin{align}
\bm{x}\in W
\to
A\bm{x}\in W
\end{align}
を満たすとき，$W$は$A$に対して不変（invariant），または$A$-不変であるというが，線形変換$A$の固有ベクトルは$A$によって定数倍されるだけであるため，$A$の固有空間はすべて$A$-不変である。
固有空間分解
ベクトル空間$V$の部分空間$V_1,V_2$の和$V_1+V_2$を
\begin{align}
V_1+V_2
=
\{v_1+v_2 \in V \ | \ v_1 \in V_1, v_2 \in V_2 \}
\end{align}
で定義する。 特に，$V_1 \cap V_2=\emptyset$であるとき，この和を直和（direct sum）といい，$V_1 \oplus V_2$と表す。
命題： $V$上の$n$次線形変換$A$が対角化可能なら，$V$は固有空間の直和に分解できる。
proof 対角化可能であるための条件より，$A$が対角化可能であるということは，$A$は$n$個の線形独立な固有ベクトルを持つということである。 これら$n$個の固有ベクトルは$V$の基底となる。 よって，$V$の任意の元はこれらのベクトルの線形結合として表せる。 このとき，これら各ベクトルに対応する固有値を$\lambda_i$，対応する固有空間を$W(\lambda_i)$とすると
\begin{align}
W(\lambda_i) \cap W(\lambda_j)=\emptyset, (i\neq j)
\end{align}
であるから
\begin{align}
V=W(\lambda_1)\oplus ...\oplus W(\lambda_n)
\end{align}
と$V$を固有空間の直和で表せる。
□
この固有空間によるベクトル空間の直和分解を，固有空間分解（eigenspace decomposition）という。