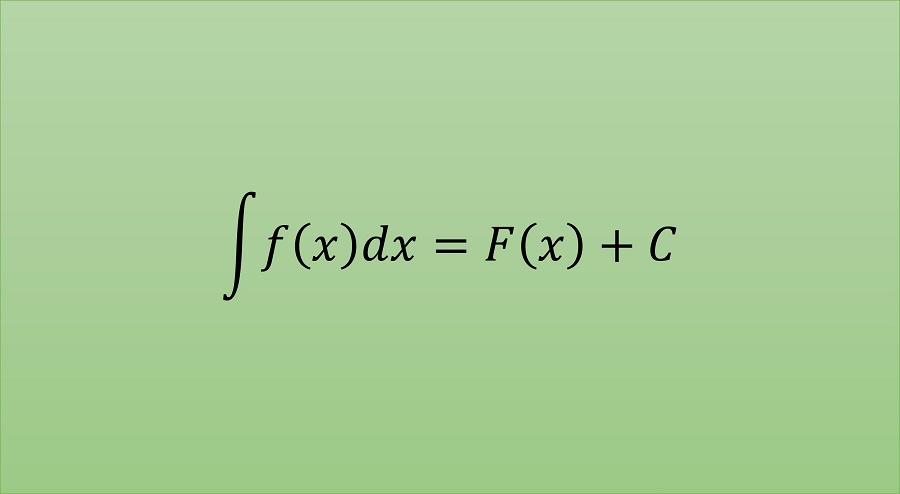内容

    1. ノート一覧
    2. 数学
    3. 微分積分

    積分の基礎

    Dr. SSS 2020/06/13 - 10:20:12 4070 微分積分
    はじめに

    ここでは，積分の基礎を簡潔に提示する。

    物理の初学者は，『積分と運動方程式の解』と合わせて読んでもらえれば，イメージがよりつかみやすくなると思う。


    keywords: 微分積分, 高校数学

    積分の考え方

    『微分の基礎』で説明したように，ある関数$f$を微分することで，導関数という別の関数$f'$が得られるのだった。 今度は，導関数$f'$から元の関数$f$を復元する操作について考える。 ちなみに，導関数に対するこの元の関数を原始関数（primitive function）という。

    関数$y=f(x)$を$xy$平面上に描いたとき，導関数$y'(x)=(df/dx)(x)$は$x$におけるグラフ$y=f(x)$の傾きを表すのだった。 傾きというのは，$x$の変化分に対する$y$の変化分であるから，$df/dx$に$x$の変化分$\Delta x$をかけたものは，$y$の変化分$\Delta y$を与える：

    \begin{equation} \label{eq:Delta_y} \Delta y = \frac{df}{dx} \Delta x \end{equation}

    したがって，ある点$x$での$y$の値に(\ref{eq:Delta_y})を加えると，「点$x$での変化率でそのまま$y$が変化していった場合の」$x+\Delta x$における$y$の値が得られる。 しかし，ある点の傾きが一定に保たれるのは$y=ax+b$（$a,b$は定数）という形で表される直線の場合だけであり，$y(x)+\Delta y$と$y(x+\Delta x)$の値は一般にずれる（図1）。

    図1：$y(x)+\Delta y$と$y(x+\Delta x)$のずれ

    このずれを小さくするには，$\Delta x$の幅を小さくしてやればよい（図2）。 そのため，幅を$\Delta x\to dx$としてやれば，$x$から無限小$dx$だけずれた部分の$y$の値が

    \begin{equation} \label{eq:y_x_dx} y(x+dx)=y(x)+\frac{dy}{dx} dx \end{equation}

    と得られる。 そこからさらに$dx$だけ離れた点$x+2dx$での$y$の値は(\ref{eq:y_x_dx})に，$x+dx$における$y$の傾きに$dx$をかけたものを加え

    \begin{equation} y(x+2dx) =y(x+dx)+\left(\frac{dy}{dx}\right)_{x+dx} dx \end{equation}

    と計算できる。

    図2：$\Delta x$を小さくしていくと，$y(x)+\Delta y$と$y(x+\Delta x)$のずれは小さくなる。

    よって，任意の点$x=x_i$からはじめ，別の点$x=x_f$までこれを繰り返せば$x_f$における$y$の値が

    \begin{equation} y(x_f) = y(x_i) + \int_{x_i}^{x_f} \frac{dy}{dx}dx \end{equation}

    と得られる。 ここで

    \begin{equation} \int_{x_i}^{x_f} \frac{dy}{dx}dx \end{equation}

    が，$x=x_i$から$x=x_f$までの各点での$df/dx$に$dx$をかけたものを足し合わせることを表しており，このような無限小区間ごとの値を足し合わせる操作を積分（integral）と呼ぶ。 特に，積分の始点と終点を定めたこのような操作を定積分（definite integral）という。 この操作は，例えば$f$が物体の位置，$x$が時間，$f'$が物体の速度であるとすれば，初期位置$f(x_i)$から物体の速度をつないで，未来の位置$f(x_f)$を導き出す操作に対応している。

    定積分の式を改めて一般的な形に表せば

    \begin{equation} \label{eq:def_int} \int_{x_i}^{x_f} f'(x) dx = f(x_f)-f(x_i) \end{equation}

    となる。

    不定積分

    定積分に対して，積分の範囲を指定せず，元の関数の形だけを求める操作を不定積分（indefinite integral）という。 微分というのはある点での変化率を求めるものであるため，例えば$y=x^2+2$という関数であれ，$y=x^2-5$という関数であれ，どちらも微分してしまえば同じ$y'=2x$という導関数が与えられる。 つまり，微分を行うと定数項の情報は失われてしまう。 よって，導関数$f'$の原始関数が$f$であるとき，$f'$の積分結果には

    \begin{equation} \int f'(x) dx=f(x)+ C \end{equation}

    と，定数項$C$を加えてやらないといけない。 定積分(\ref{eq:def_int})の場合は，この積分の結果に積分範囲の両端の値を入れたものの差を取るため

    \begin{equation} (f(x_f)+C) - (f(x_i) +C) = f(x_f) - f(x_i) \end{equation}

    と$C$はキャンセルし，考慮する必要がなかった。 こうしたことから，ある関数$f$の原始関数を$F$としたとき，$f$の不定積分の結果は不定な定数$C$を含むものとして

    \begin{equation} \int f(x) dx =F(x)+C \end{equation}

    と表される。

    積分計算の例

    これまで説明したように，積分は導関数から元の関数を求める操作である。 よって例えば，$x^a$という形の関数に関しては

    \begin{equation} (x^a)'=ax^{a-1} \end{equation}

    より

    \begin{equation} \int x^a dx = \frac{x^{a+1}}{a+1}+C, \quad (a\neq -1) \end{equation}

    という公式が得られる。

    同様に，三角関数や指数関数，対数関数に関して

    \begin{align} \int \sin{ax} \ dx = -\frac{1}{a}\cos{ax}+ C , \ \ (a\neq 0) \\ % \int \cos{ax} \ dx = \frac{1}{a}\sin{ax}+ C , \ \ (a\neq 0) \\ % \int e^{ax} \ dx = \frac{1}{a}e^{ax}+ C , \ \ (a\neq 0) \\ % \int \frac{1}{x}dx = \log{|x|}+C \end{align}

    などの公式が得られる。

    部分積分

    関数の積の微分について

    \begin{equation} \{ f(x) g(x) \}' =f'(x)g(x)+f(x)g'(x) \end{equation}

    という公式が成り立つのだった（忘れた人はコチラで確認）。 これを積分すると

    \begin{equation} f(x) g(x) =\int f'(x)g(x) dx + \int f(x)g'(x) dx \end{equation}

    となる。 よって順番を入れ替えることで

    \begin{equation} \int f'(x)g(x) dx = f(x) g(x) - \int f(x)g'(x) dx \end{equation}

    という公式が得られる。 このような変形を行うこと，部分積分（integration by parts）を行うという。 部分積分の有用さは，学習を進めるうえで実際に適用してみると直ちに理解できるだろう。

    参考文献

    目次

    微分積分の基礎

    多変数関数の微分積分