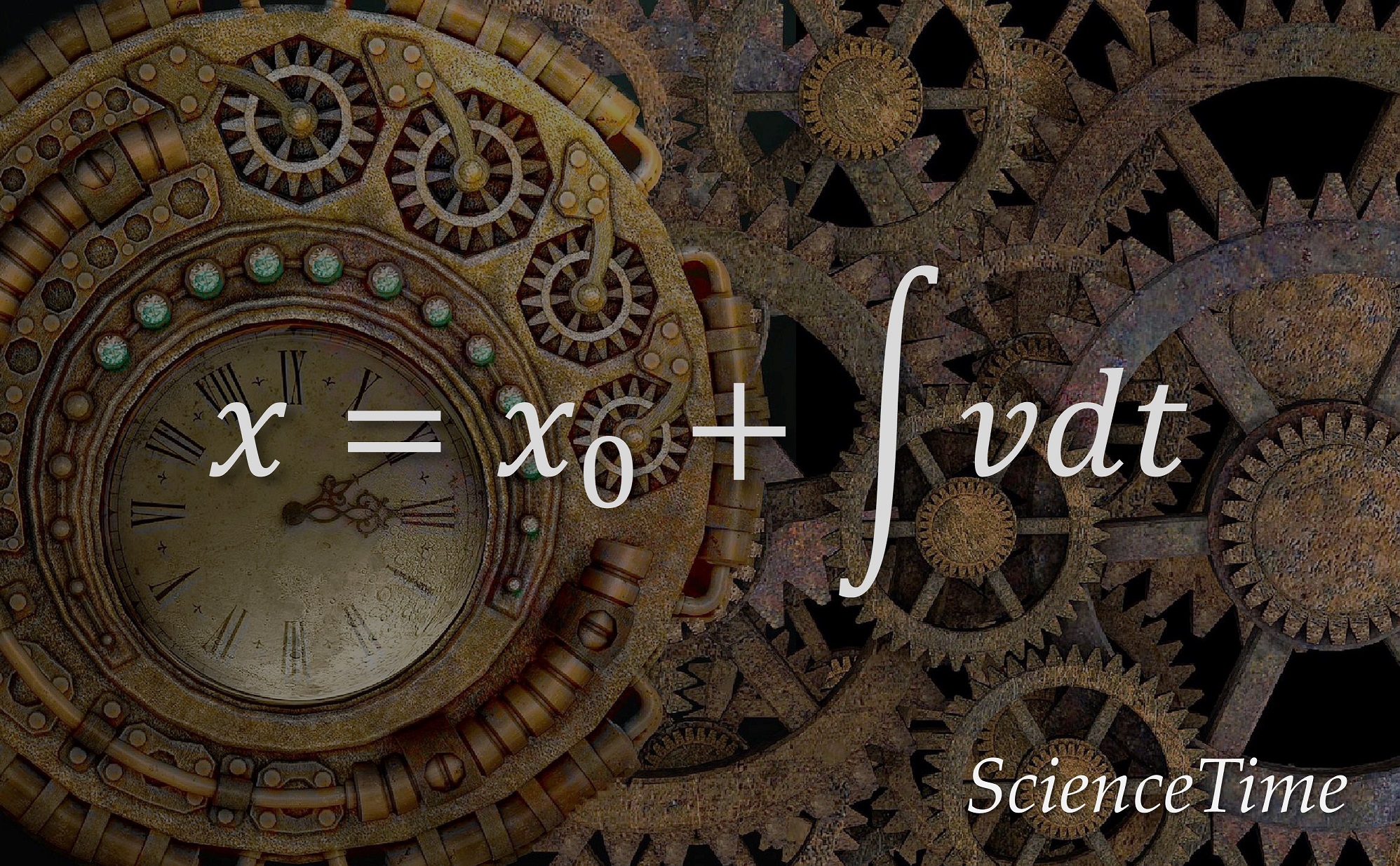積分と運動方程式の解

はじめに

『微分とNewtonの運動方程式』では，微分という操作と，Newtonの運動方程式について触れた。ここでは，微分の反対の操作である積分と，それを用いてNewtonの運動方程式の解を求める手順を簡単な例によって示す。

keywords: 運動方程式, 微分積分, 高校数学, Isaac Newton, 古典力学, Pierre-Simon Laplace, Newton力学

内容

積分の考え方

『微分とNewtonの運動方程式』に引き続いて，直線上で問題を考えよう。直線上を正の方向に時速60km/hを保って車が走っているとする。この車が1時間走ったらどれだけの距離を進むだろうか？答えは簡単で

\begin{align} {\rm 距離} = {\rm (速さ)}\times{\rm (時間)}= {\rm 60 \ [km/h]}\times {\rm 1 \ [h]} = {\rm 60 \ [km]} \end{align}

である。この関係は，進んだ距離を$\Delta x$，速度を$v$，かかった時間を$\Delta t$とすれば

\begin{align} \Delta x = v\Delta t \end{align}

と一般化できる。しかし，この関係で正しい距離が得られるのは，$\Delta t$の間速度$v$が一定である場合だけである。では現実に走っている車のように，刻々と速度が変化する場合にはどのようにしたら進んだ距離が求められ，任意の時刻における位置を知ることができるだろうか？

そのためには，微分の場合同様，その間に速度が変化しないくらい$\Delta t$を十分小さくとってやればいい。だがその前にまず，今考えた例を少し変形させた問題を考えてみよう。次は10分ごとに車の速度が変化するとする。それに対応して，時間$t$が取る0から1時間の範囲を6分割し，各区間の最初の時刻（0，10分，20分…50分）を，$t_0,t_1,...,t_5$と表す。60分後は$t_6$としよう。 $\Delta t$の幅はこの場合1時間ではなく10分に取る。そして，各区間での速度は$v_0=v(t_0),...,v_5=v(t_5)$と表す。すると，各区間ごとに進む距離$\Delta x_0,...,\Delta x_5$は

\begin{align} \Delta x_0= v_0 \Delta t, \ \ \Delta x_1 = v_1 \Delta t, ..., \Delta x_5 = v_5 \Delta t, \end{align}

と表せる。そして，この$\Delta x_i$をすべて足し合わせたものが1時間の間に進む距離$\Delta x$となる：

\begin{align} \notag \Delta x= \Delta x_0+ \Delta x_1 +...+ \Delta x_5 =& \sum_{i=0}^5 \Delta x_i \\ =& \sum_{i=0}^5 v_i \Delta t \end{align}

ここで記号$\sum_{i=0}^5$は，$i$に0から5を入れて足し合わせるという操作を表している。これを表したのが，以下の図1である。もともと連続的である軌道を赤色の曲線で示し，それを6つの曲線で近似している。

図1：赤色の曲線で表される連続的な運動を，6つの直線で近似した図

図1を見てわかるのは，$t_i, i=0,...,6$以外の時刻では，元の軌道を表す赤色の曲線と，近似直線の間にずれがあるということである。そのため，例えば$t_0$から$t_3$と$t_4$の中間の時刻までに進んだ距離を知りたいと思っても，今の近似では正確に求めることができない。

任意の時間でより高い精度の答えが得られるようにするためには，分割する時間幅をもっと小さく取ってやればいい。すると，任意の軌道に適用できる一般化した形を次のように得ることが出来る：

\begin{align} \notag x=\lim_{\Delta t \to 0} \sum_{i} v_i \Delta t \end{align}

和の記号$\sum$の下の添え字のみを記しているが，この場合，$v_i$が全部でどれだけあるかわからないけどとにかく全部足すということを意味している。ここでは極限操作によって，$\Delta t$が0に近づいていくに連れて足し合わせる数はどんどん増していき，最終的には無限個足し合わせることになる。この操作を表すのが積分であり，次のように記される：

\begin{align} \label {def:int} \int_{t_0}^{t_f} v(t)dt \equiv \lim_{\Delta t \to 0} \sum_{i} v_i \Delta t \end{align}

これが時刻$t_0$から$t_f$までに進んだ距離に等しくなる。

積分計算の仕方

微分の場合と同じように具体例を考えてみよう。この場合も$x(t)=t^2$，すなわち$v(t)=dx/dt=2t$であるとする。前者を微分したものが後者であり，積分はその逆の操作であることから

\begin{align} \label{int_ex} \int 2t dt =t^2 +C \end{align}

という結果が得られる。ここで，$C$は積分定数と呼ばれる定数である。今の場合，$t=0$とした場合の位置，すなわち初期位置に対応する。位置の微分である速度は，位置の瞬間的な時間変化率を表すものであるため，初期位置のような情報は失われている。そのため，導関数から元の関数（原始関数と呼ばれる）を積分によって復元するときは，積分定数としてそのような失われた情報を手で足してやらないといけない。このように，積分範囲を指定せず，原始関数を求める操作を，不定積分という。

今の例の一般化として，微分公式

\begin{align} \frac{d}{dt}t^{\alpha }=\alpha t^{\alpha-1}, \ \ \alpha \text{は実数} \end{align}

に対応し

\begin{align} \int t^\alpha dt =&\frac{t^{\alpha+1}}{\alpha+1} +C \\ （\alpha \neq & -1） \notag \end{align}

という公式が得られる。

不定積分に対し，(\ref{def:int})のように，積分の下限（初期時刻$t_0$に対応）と，上限（終時刻$t_f$に対応）を決め，それらの間の差を計算するものを，定積分という。 $v(t)=2t$で運動する物体が時刻$t_0$から$t_f$までに進む距離は，(\ref{int_ex})に$t=t_f$および$t=t_0$を代入した結果の差として

\begin{align} \int_{t_0}^{t_f} 2t dt = \left. t^2 \right|^{t_f}_{t_0} = (t_f^2 +C)- (t_0^2+C) = t_f^2 - t_0^2 \end{align}

と計算される。このように，定積分では積分定数$C$は打ち消され，結果に寄与しないことに注意しよう。

運動方程式の積分：自由落下の例

前節までの考え方にしたがって，実際にNewtonの運動方程式

\begin{align} \label {Neweq} m\frac{d^2x}{dt^2} =F \end{align}

の簡単な例を解いてみよう。引き続き問題は1次元に限定する。今回力は$F=-mg$と選択する。ここで$m$は考えている物体の質量，$g$は定数である。すると(\ref{Neweq})は

\begin{align} \label {graveq} m\frac{d^2x}{dt^2} =-mg \end{align}

となる。これは，物体が重力$mg$のみの影響下で行う運動，いわゆる自由落下を記述する方程式と同じ形だ。なので$x$は鉛直方向の座標，$g$は重力加速度と考えて話を進めよう。まず(\ref{graveq})の両辺に質量$m$がかかっているのでそれを削ぎ落してしまえば

\begin{align} \frac{d^2x}{dt^2} =-g \end{align}

となる。あとはこれを積分するだけである。$x$を取り戻すには2回時間について積分する必要があるが，まず1回目の形は

\begin{align} \int \frac{d^2x}{dt^2} dt =-\int g dt \end{align}

となる。先に述べたように$g$は定数であって時間によらないから，$dt$を積み上げた後に最後にかけ合わせてやればよく，$-\int g dt=-g\int dt$とできる。そしてこの結果に積分定数が1つ現れるから，それを$v_0$とすれば，この積分の結果は

\begin{align} \frac{dx}{dt} =-gt+v_0 \end{align}

となる。どうしてこうなるかわからない場合は，これをもう一度時間で微分して(\ref{graveq})になることを確かめるといい。後はもう1回積分するだけで，その時の積分定数を$x_0$とすれば

\begin{align} x(t) =-\frac{1}{2}gt^2+v_0 t + x_0 \end{align}

が得られる。$x(0)=x_0$であるから$x_0$は初期位置であり，$v_0$は初期速度である。$v_0$が正なら，$x_0$の位置から時間$t$に比例して上に向かってどんどん上昇して行こうとするのだが，$t^2$に比例する重力によって下に引き戻されるということを意味している。もし$v_0$が十分大きければ，物体は地球の重力を振り切って宇宙の彼方へ飛んでいくことになるが，反対にそれ以下の大きさなら，やがて最高点で向きを変え落下してくる。単に初速度0で手から物を落とした場合も同じ運動方程式に従うわけだが，このような単純な方程式でも，初期条件によってこれだけ劇的に振る舞いが変わりうるのである。

このような自由落下のケースに限らず，Newtonの運動方程式は2階の微分方程式であるから，2度の積分に伴う積分定数に対応して2つの初期条件が必要とされる（Newton力学とは別の形式もあるがこの事情は変わらない）。しかし言い換えれば，物体に加わる力と初期条件さえ分かれば，それを実際に解くことができるかは別として，原理的には運動方程式によってその物体の運命は完全に決定できてしまう。古典力学的な世界はこうした物体の集まりとそれらの間の相互作用（物体同士には力として働く）で出来ているのだから，もしすべての物体の力学的状態（位置と速度）とそこに作用する力を知り運動方程式を解く知性があれば，世界全体の未来，そして遡って過去までも知り尽くすことが，原理的には可能である。これを指摘した人物であるLaplaceにちなんで，この仮想的な知性はLaplaceの悪魔と呼ばれている。

積分と運動方程式の解

積分の考え方

積分計算の仕方

運動方程式の積分：自由落下の例

参考文献