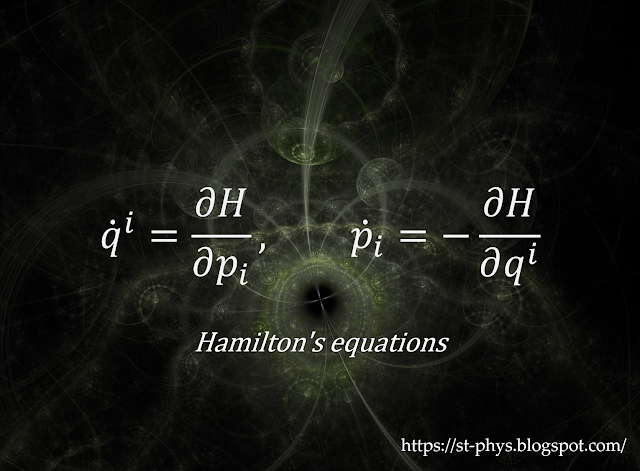Introduction
Lagrange形式からHamilton形式に移行する手続きを解説する。
Legendre変換の一般的方法や意味,あるいは一般化速度と一般化運動量の幾何学的性質の違いなどの説明は別で行う。
復習:一般化運動量
Lagrange形式の力学の利点の一つは,保存量の見えやすさである。
例えばLagrangianが平行移動$L(q)\to L(q+\epsilon)$で不変に保たれるとき,すなわち
\begin{equation}
\sum_i \frac{\pd L}{\pd q^i} \ep^i =0
\end{equation}
のとき,Euler-Lagrange方程式
\begin{equation}
\label{eq:E-L_eq}
\frac{d}{dt}\frac{\pd L}{\pd{\dot{q}}^i}=\frac{\pd L}{\pd q^i},
\end{equation}
より
\begin{equation}
\label{eq:p_consv}
\sum_i \frac{d}{dt}\frac{\pd L}{\pd{\dot{q}}^i}=0,
\end{equation}
となり,$\pd L/\pd \dot{q}^i$の総和は保存量であることがわかる。
ここで
\begin{equation}
\label{eq:def_p}
p_i(q,\dot{q},t)\equiv \frac{\pd L}{\pd{\dot{q}}^i},
\end{equation}
は$q^i$に共役な一般化運動量(generalized momentum)と呼ばれ,(\ref{eq:p_consv})は一般化された運動量保存則に対応する。
一般化運動量は$q^i$がCartesian座標でない場合,一般に線形運動量と同じ次元を持たないし,例えば磁場中の荷電粒子のように速度に依存するポテンシャルを持つ場合,$q^i$がCartesian座標であっても力学的運動量$mv$とは一致しない。
Hamiltonianと相空間
Lagrangianは簡単のため時間に陽に依存しないとすると,Lagrangianの全微分は一般化運動量を用いて
\begin{equation}
\label{eq:dL}
\begin{split}
dL
=& \frac{\pd L}{\pd q^i} dq^i +\frac{\pd L}{\pd \dot{q}^i} d \dot{q}^i \\
=& \dot{p}_i d q^i + p_i d \dot{q}^i
\end{split}
\end{equation}
と表せる。
ここEuler-Lagrange方程式(\ref{eq:E-L_eq})より
\begin{equation}
\frac{\pd L}{\pd q^i}
= \frac{d}{dt}\frac{\pd L}{\pd{\dot{q}}^i} = \frac{d}{dt} p_i
\end{equation}
であることを用いた。
(\ref{eq:dL})の第2項を
\begin{equation}
p_i d \dot{q}^i
=d(p_i \dot{q}^i)-\dot{q}^i dp_i
\end{equation}
とし,並び変えることで
\begin{equation}
\label{eq:dH}
d\left( p_i \dot{q}^i-L\right)
=- \dot{p}_i d q^i + \dot{q}_i d p_i
\end{equation}
を得る。つまりこの式は,一般化運動量(\ref{eq:def_p})が定義できるとき,$q$と$p$の関数
\begin{equation}
\label{eq:def_hamiltonian}
H(q,p)
\equiv p_i \dot{q}^i-L
\end{equation}
が存在することを表している。
この関数$H$をHamiltonianという。
改めて,Hamiltonianは$q$と$p$を独立変数とする関数であり,$(q,p)$を座標とする空間を相空間(phase space)という。
このとき,$q$と$p$は正準座標(canonical coordinates)と呼ばれる。
(\ref{eq:dH})はHamiltonianの全微分であるから
\begin{equation}
\label{eq:canonical_equations}
\frac{dq^i}{dt}
= \frac{\partial H}{\partial p_i},
\quad
\frac{dp_i}{dt}
=-\frac{\partial H}{\partial q^i}
\end{equation}
を得る。
これらをHamilton方程式(Hamilton's equations),あるいは正準方程式(canonical equations)という。
相空間上の作用
Hamiltonianの定義(\ref{eq:def_hamiltonian})より,作用を
\begin{equation}
\begin{split}
S
=&
\int_{t_1}^{t_2} L dt \\
=&
\int_{t_1}^{t_2}
\left(\sum_i p_i\frac{dq^i}{dt}-H\right)dt \\
=&
\int (\sum_i p_idq^i-Hdt)
\end{split}
\end{equation}
と表すことができる。
ここで,$dq^i$の積分は$dq^i(t_1)$から$dq^i(t_2)$までである。
この変分がゼロであるという条件から,粒子の軌道が決まるわけであるが,今は相空間上の関数として作用を考えているから,$q$と$p$の変分それぞれ独立に扱わなければならない。
境界条件は,配位空間上と同様に,$\delta q_i=0$とし,変分を取ると
\begin{equation}
\label{eq:delta_S_hamiltonian}
\begin{split}
\delta S
=&
\int (\sum_i p_idq^i-Hdt) \\
%
=&
\int \sum_i \left[\delta p_i dq^i + p_i d\delta q^i
-\frac{\pd H}{\pd q^i}\delta q^i dt
-\frac{\pd H}{\pd p_i}\delta p_i dt
\right] \\
%
=&
\int \sum_i\left[
\delta p_i \left(dq^i -\frac{\pd H}{\pd p_i} dt \right)
-\delta q^i \left(dp_i + \frac{\pd H}{\pd q^i} dt \right)
\right]
\end{split}
\end{equation}
となる。
途中で$p_i d\delta q^i=d(p_i \delta q^i)-dp_i \delta q^i$および,境界で$\delta q_i=0$であることを用いた。
改めて,変分$\delta q^i$と$\delta p^i$は独立であるから,(\ref{eq:delta_S_hamiltonian})がゼロであるためには,それぞれの係数がゼロでなくてはらない。
この条件は,正準方程式(\ref{eq:canonical_equations})と等価である。
References
Landau, L. D., & Lifshitz, E. M. (1976). Mechanics third edition: Volume 1 (Course of Theoretical Physics). Elsevier Science
――(1986). 力学 (ランダウ=リフシッツ理論物理学教程). 広重 徹, 水戸 巌 訳. 東京図書.
山本 義隆 & 中村 孔一. (1998). 解析力学I&II. 朝倉書店.
米谷 民明. (1993). 力学. 培風館.