変分法：2点間の最短距離

はじめに

物理学において非常に重要な役割を果たす変分法を，単純かつ具体的な例を通して説明する。Lagrange力学やHamilton力学を学ぶ際に

変分て何？微分とどう違う？
汎関数て何？関数とどう違う？
曲線（軌道）の座標とその傾き（速度）を独立変数とみなすとはどういう意味？

といったことに困っている人たちの疑問解消にもなるよう努めた。個人的な観測では，特にこの3つ目の疑問に明確ですっきりとした回答を与えているテキストは少ない。

keywords: 数学, Lagrange力学, 変分法, 解析力学, 最小作用の原理, 変分原理

内容

曲線の全長

平面内の固定された2点を，最も短い長さで結ぶ曲線は何か，という問題を考える。平面内の線素は

\begin{equation} ds=\sqrt{ dx^2+dy^2} \end{equation}

であるため，始点$A$から終点$B$まで積分することで，始点と終点を結ぶ曲線の全長は

\begin{equation} \label{eq:S_path} S =\int_{A}^{B} ds =\int_{x_A}^{x_B} \sqrt{1 + \left( \frac{dy}{dx} \right)^2} dx \end{equation}

となる。この被積分関数を，一般的な形として，$x$と$y$および$y'=dy/dx$の関数として $$ F(x,y,y') $$ で表せば，(\ref{eq:S_path})は

\begin{equation} \label{eq:S_act} S[y] = \int_{x_A}^{x_B} F(x,y,y') dx \end{equation}

$y$と$y'$を独立変数とできる理由は最後に説明する。

汎関数と変分法

関数$y=f(x)$というのは，$x$の値に$y$の値を対応させる規則のことであるが，この固定された2点を結ぶ曲線の長さを表す$S$は，関数$F$の形によって値が決まる。このような関数は，汎関数（functional）と呼ばれ，関数と区別するため，(\ref{eq:S_act})のように，表記に丸括弧ではなく角括弧が用いられたりする。つまり，2点間を最短で結ぶ曲線を見つける問題というのは，汎関数(\ref{eq:S_act})を最小にする関数$F(x,y,y')$の形を決めることだということになる。以下，変分法といったテクニックを用いてこの問題を解く手順を説明するが，あくまで最短距離の問題は理解のための具体例であり，基本的な議論は一般の場合にも成り立つ。

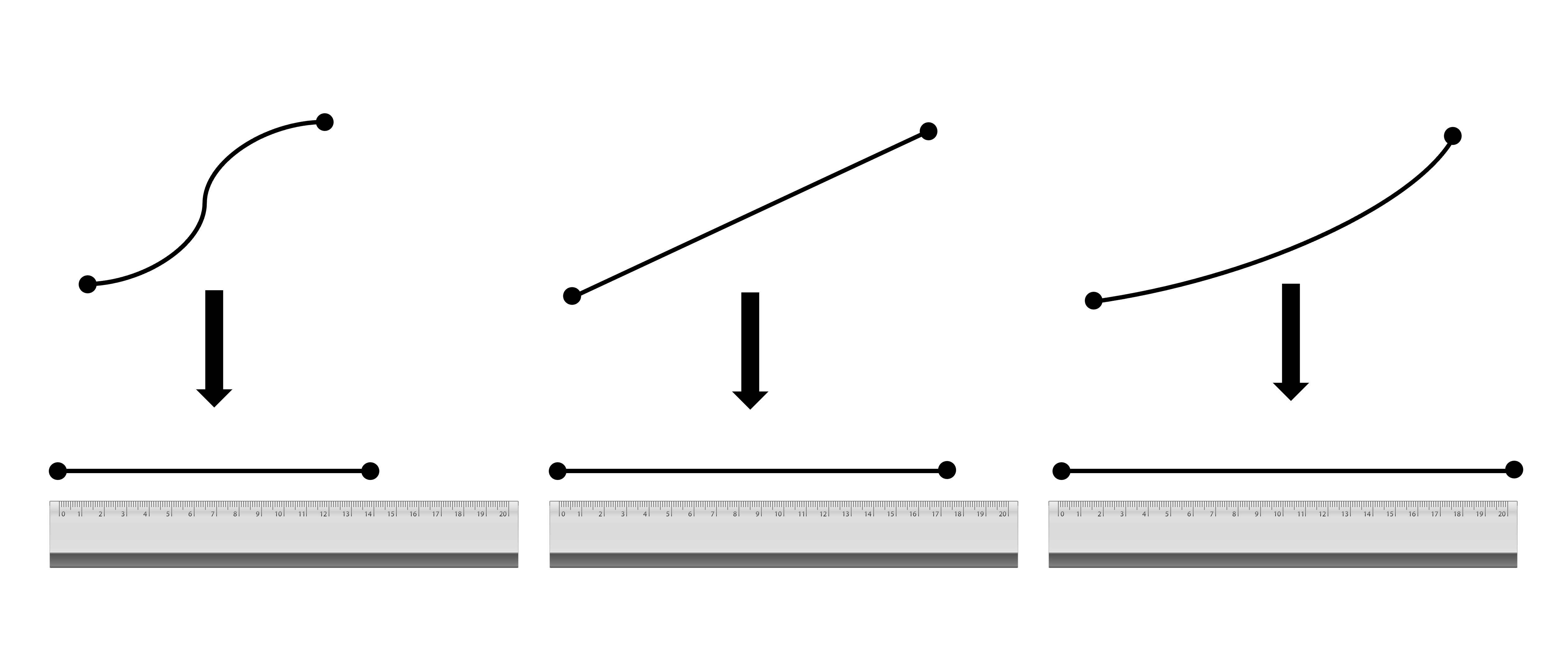
図1

汎関数$S$の値は，$f$がパラメータ$x$に対して具体的にどんな値を取るかということではなく，$f$がどんな形をしているかによって決まる。ある関数$f(x)$が$x_0$で停留値を取るとき，すなわち$(df/dx)_{x=x_0}=0$となるとき，その付近任意で無限小な関数$\delta x$を加え，$x$の値を$x_0+\delta x$と変化させても

\begin{equation} f(x_0+\delta x)=f(x_0)+\frac{df(x_0)}{dx}\delta x+O(\delta x^2) \end{equation}

より，$\delta x$の一次の範囲で$f$は変化しない。そのため，汎関数$S$を最小にする$F$の形をわずかに変更させても$S$の値は変化しないはずである。言い換えると，今考えている問題の場合，$F(x,y+\delta y,y'+\delta y)$と変数を独立に，わずかに変化させた場合の$S[y+\delta y]$と元の$S[y]$の差

\begin{equation} \label{eq:del_S} \delta S = \int_{x_A}^{x_B} F(x,y+\delta y,y' + \delta y') dx -\int_{x_A}^{x_B} F(x,y,y') dx \end{equation}

が$0$になる関数$F$を見つければよいということである。

改めて，ここで$\delta x$や$\delta y$などは，単に関数を平行移動しているのではなく，適当な関数を加えて関数の形自体を変化させているということには注意してほしい。例えば$F=x^2$という簡単な2次曲線であった場合，無限小のパラメータ$\ep$を用いて$\ep x^3$といった関数を作って加え，$F=x^2+ \ep x^3$などとしてしまってもいい。この微小な関数を変分（variation）といい，変分を用いて（汎）関数の極値や停留値を見出す分野を変分法（variational method）という。

ここで多くの人が疑問に思うのが，なぜ$y$とその導関数$y'$を関数$F$の独立変数として選択しておきながら，変分$\delta y$を加えたときに$y'$まで変化させるのか，ということである。これについては，最後の節で説明する。

Euler方程式

さて，(\ref{eq:del_S})の被積分関数の差は，微小量の一次までで

\begin{equation} F(x,y+\delta y,y' + \delta y') -F(x,y,y') = \frac{\pd F(x,y,y')}{\pd y}\delta y +\frac{\pd F(x,y,y')}{\pd y'}\delta y' \end{equation}

であるから(\ref{eq:del_S})は

\begin{equation} \delta S = \int_{x_A}^{x_B} \left[\frac{\pd F(x,y,y')}{\pd y}\delta y +\frac{\pd F(x,y,y')}{\pd y'}\delta y' \right]dx \end{equation}

と変形できる。そして

\begin{equation} \delta y'=(y+\delta y)'-y' =\frac{d}{dx} \delta y \end{equation}

を用いて，括弧内2項目を部分積分することで

\begin{equation} \label{eq:S_part_int} \delta S = \int_{x_A}^{x_B} dx \left[ \frac{\pd F(x,y,y')}{\pd y} - \frac{d}{dx} \frac{\pd F(x,y,y')}{\pd y'} \right]\delta y +\left[ \frac{\pd F(x,y,y')}{\pd y'}\delta y \right]_{x_A}^{x_B} \end{equation}

となり，最後の項は，両端を固定しているという条件，すなわち$\delta y(x_A)=\delta y(x_B)=0$より消える。そして変分$\delta y$が任意であったことから，(\ref{eq:S_part_int})がゼロであるためには

\begin{equation} \label{eq:eul_eq} \frac{\pd F(x,y,y')}{\pd y} - \frac{d}{dx}\frac{\pd F(x,y,y')}{\pd y'} = 0 \end{equation}

が成り立つ必要があることがわかる。この式をEuler方程式と呼ぶ。

今考えている例では

\begin{equation} \frac{\pd F}{\pd y} = 0, \quad \frac{\pd F}{\pd y'} = \frac{y'}{\sqrt{1+y'^2}} \end{equation}

であるから，Euler方程式(\ref{eq:eul_eq})は

\begin{equation} \frac{d}{dx} \frac{y'}{\sqrt{1+y'^2}} =0 \to \frac{d y'}{dx} =0 \end{equation}

となり，解は定数$a$，$b$を用いて

\begin{equation} y=ax+b \end{equation}

と表せることがわかる。つまり，平面内の二点を繋ぐ最も短い曲線は直線でることが確かめられる。 $a$，$b$は中学だか高校でやらされるように，始点と終点を通るように選択される。

微分と変分

改めて，微分と変分の違いについてもう少し詳しく考えてみる。関数$y=f(x)$というのは，パラメータ$x$に値$y$を対応させる規則であったが，このとき$y$と傾き$y'=dy/dx$は独立な変数としてみなせるということを明確にしよう。

傾き$y'$というのは，パラメータ$x$がわずかに異なる$y$の値の差から決まる量であるが，これは，ある特定のパラメータ$x$の値に対して$y$の値がどうだということとは直接に関係がない。例えば，ある関数$y$をそのまま平行移動すると，$y$の値は変化するが，対応するパラメータ$x$に関して$y'$の値は変化しない。この意味で，$y'$はパラメータ$x$の関数であって，$y$の関数ではない。

このことをわかりやすくするために，仮に，$y'(y,x)$と変数を取ったとしよう。これを，$y$で微分すると確かに

\begin{equation} \left( \frac{\pd y'}{\pd y} \right)_x = 0 \end{equation}

となることが，図2からもわかるだろう。

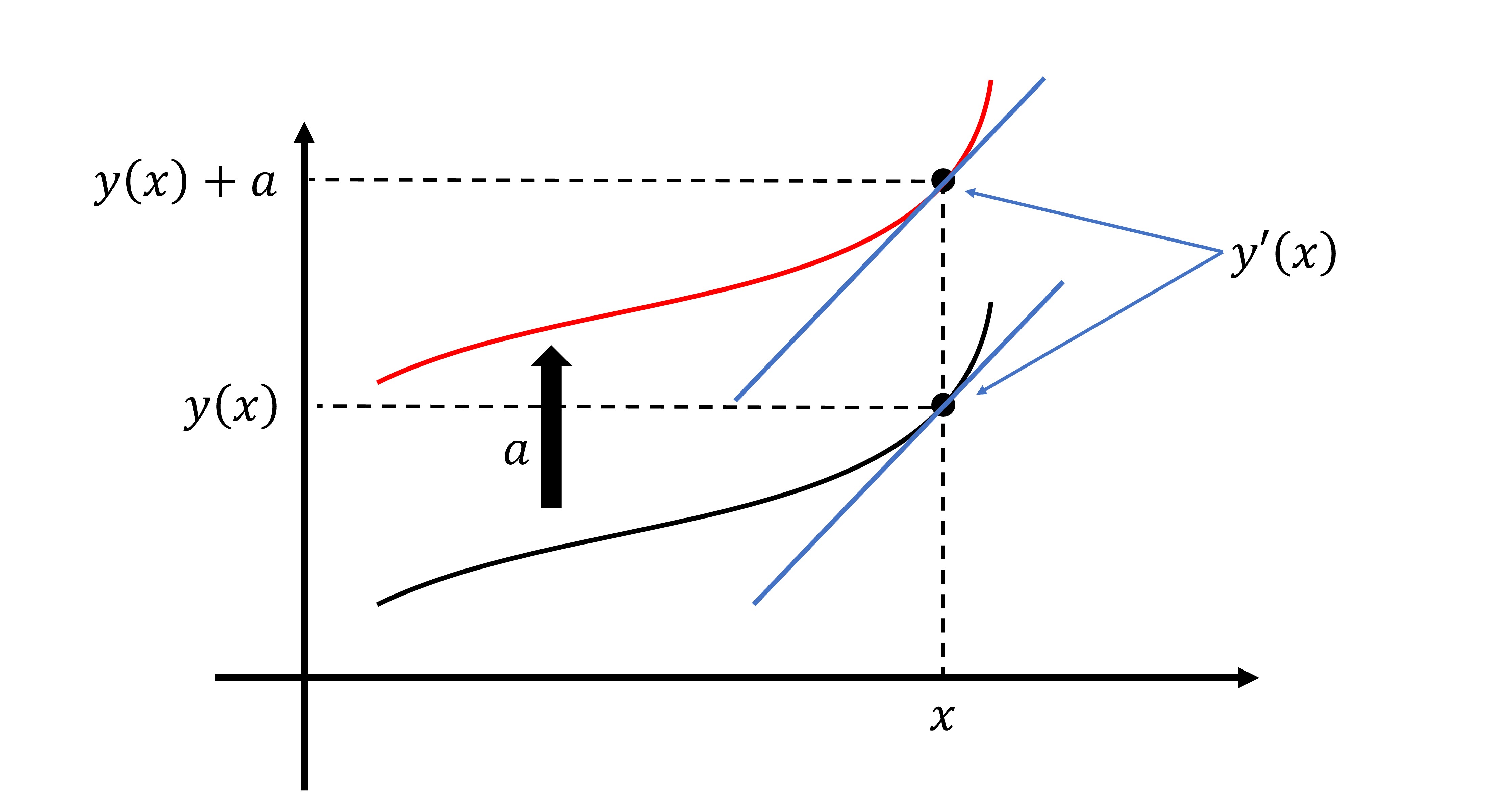
図2：平行移動をして$y$の値は変わっても$y'$の値は変わらない。また，$x$を固定して$y'$を$y$について微分することは，同じパラメータ$x$の値における元の関数と，平行移動した関数の傾きとの差を取ることに対応するから，$0$になる。

一方で，変分$\delta y$というのは，任意の関数$g(x)$と微小パラメータ$\epsilon$を使って$\delta y=\epsilon g(x)$と書けるものであるから，関数$f(x)$の形自体を変えてしまう。そのため，曲線の形が変わり，その傾きも変化する。これが，$y$と$y'$がそれぞれ関数$F$の独立変数として選択されるが，変分の際には$y$の変化だけでなく，$y'$が$y$の微分であることが明示的に利用され，$y'$の変化も考慮される理由である。

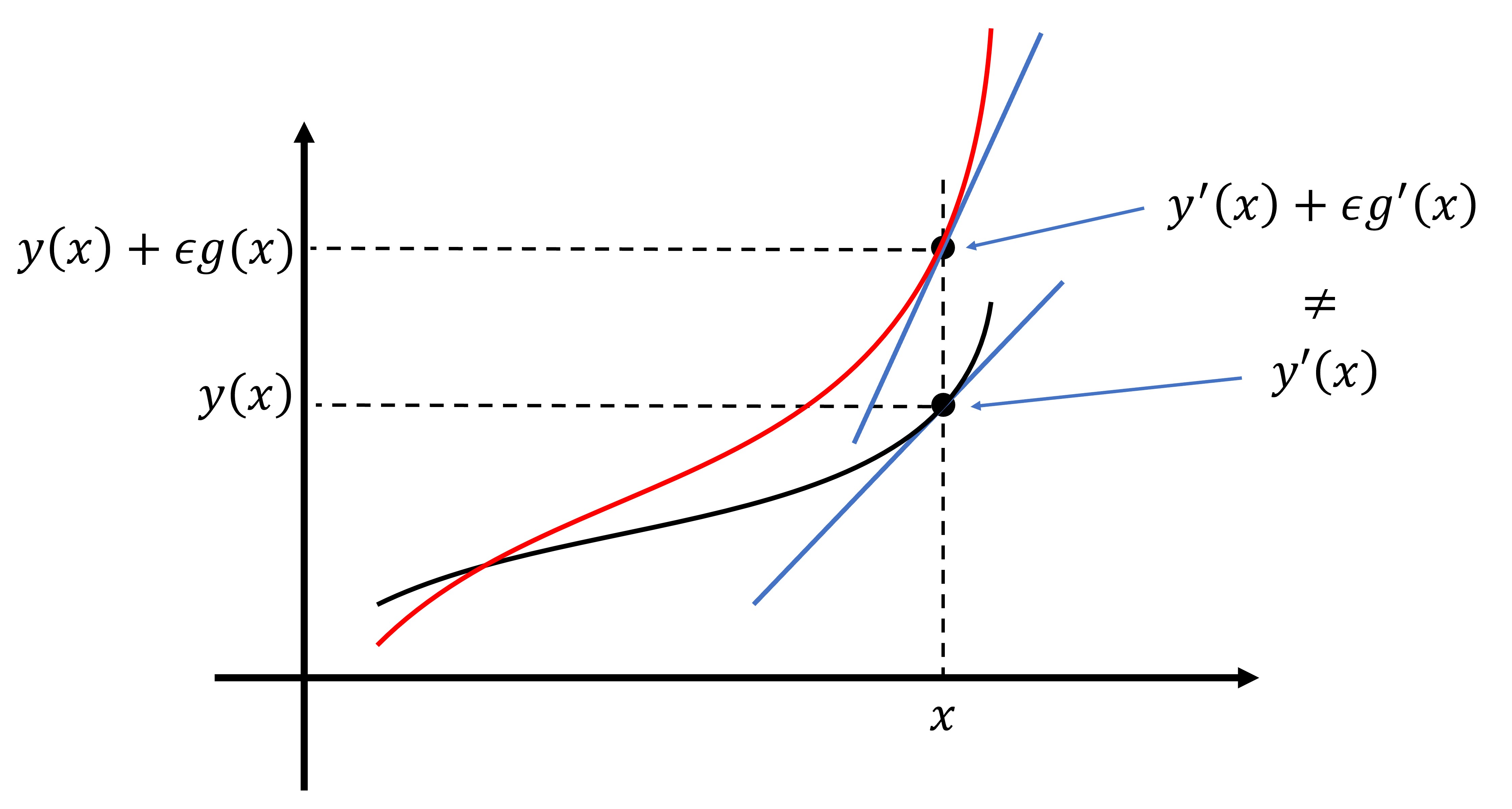
図3：変分は単なる平行移動とは異なり，関数形そのものを変えてしまうから，一般に関数の導関数も変化する。

ちなみに，これの特殊なケースとして$\epsilon g(x)=a$という定数$a$を付加するだけのケース，すなわち平行移動を考えることができる。その場合，確かに

\begin{equation} \frac{d}{dx}(y+\delta y)=\frac{d}{dx}(y+\ep a) = y' \end{equation}

となり，改めて，傾きは変化しないことが確認できる。

まとめ

重要な部分を改めて述べる： $y$の値を変化させたら，$y'$も変化しそうなものだが，それは曲線$y$に沿って移動したときの話であり，その移動を制御するのが，パラメータ$x$なのである。そして，ある点の近傍の$y$の値はそのままに，その点の$y$の値だけを変化させても$y'$の値は変化するが，それはつまり関数の形を変えているということであり，微分ではなく変分を行っていることになる。そしてその場合，確かに$y'$の値は変化するのである。

ここでの議論をLagrange力学における最小作用の原理に適用するなら，パラメータ$x$を時間$t$に，関数$y=f(x)$を軌道$q(t)$に，傾き$y'(x)$を速度$\dot{q}(t)$に，そして関数$F(y,y',t)$をLagrangian $L(q,\dot{q},t)$置き換えてやればいい。

変分法：2点間の最短距離

曲線の全長

汎関数と変分法

Euler方程式

微分と変分

まとめ

参考文献