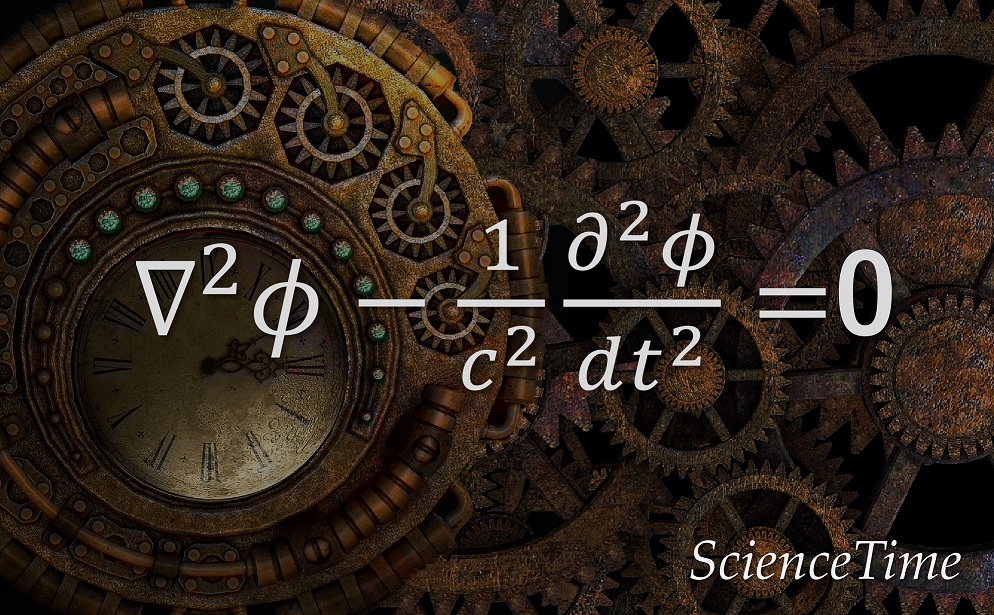はじめに
特定の方向，そちらを$x$軸に取ろう，に沿って速さ$c$で伝播する波は，1次元波動方程式
\begin{equation}
\label{eq:wave_equation}
\frac{\pd^2\phi}{\pd x^2}
-\frac{1}{c^2}\frac{\pd^2\phi}{\pd t^2}
=0
\end{equation}
によって記述される。
ここでは，弦の振動なのか音波なのか電磁波なのか，など具体的な現象は指定せず，波動方程式の一般的性質について解説する。
keywords:
波動,
波,
波動方程式,
分散関係
内容
波動方程式の一般解の形
波動方程式(\ref{eq:wave_equation})の一般解を得るため，まず変数を$(x,t)$から
\begin{equation}
\xi(x,t) = x-ct,
\quad
\eta(x,t) = x+ct
\end{equation}
に変換する。
この逆変換は
\begin{equation}
x=\frac{1}{2}(\xi+\eta),
\quad
t=\frac{1}{2}(-\xi+\eta)
\end{equation}
であるから，微分演算子は
\begin{equation}
\begin{split}
\frac{\pd}{\pd\xi}
=&
\left(\frac{\pd x}{\pd \xi}\right)_\eta
\left(\frac{\pd}{\pd x}\right)_t
+
\left(\frac{\pd t}{\pd \xi}\right)_\eta
\left(\frac{\pd}{\pd t}\right)_x \\
%
=&
\frac{1}{2}
\left(
\frac{\pd}{\pd x}
-
\frac{1}{c}
\frac{\pd}{\pd t}
\right)
\end{split}
\end{equation}
\begin{equation}
\begin{split}
\frac{\pd}{\pd\eta}
=&
\left(\frac{\pd x}{\pd \eta}\right)_\xi
\left(\frac{\pd}{\pd x}\right)_t
+
\left(\frac{\pd t}{\pd \eta}\right)_\xi \left(\frac{\pd}{\pd t}\right)_x \\
%
=&
\frac{1}{2}
\left(
\frac{\pd}{\pd x}
+
\frac{1}{c}
\frac{\pd}{\pd t}
\right)
\end{split}
\end{equation}
となる。
よって，これら新たな変数を用いると
\begin{equation}
\label{eq:decompose_wave_eq_operator}
\begin{split}
4\frac{\pd^2}{\pd\xi\pd\eta}
=&
\left(\frac{\pd}{\pd x}
-\frac{1}{c}\frac{\pd}{\pd t}\right)
\left(\frac{\pd}{\pd x}
+\frac{1}{c}\frac{\pd}{\pd t}\right) \\
%
=&
\frac{\pd^2}{\pd x^2}
-\frac{1}{c}\frac{\pd}{\pd t}\frac{\pd}{\pd x}
+\frac{1}{c}\frac{\pd}{\pd x}\frac{\pd}{\pd t}
-\frac{1}{c^2}\frac{\pd^2}{\pd t^2} \\
%
=&
\frac{\pd^2}{\pd x^2}
-\frac{1}{c^2}\frac{\pd^2}{\pd t^2}
\end{split}
\end{equation}
より，波動方程式は
\begin{equation}
\frac{\pd^2\phi}{\pd\xi\pd\eta}
=0
\end{equation}
と表される。
これを$\xi$で積分すると，$\xi$によらない関数
\begin{equation}
\label{eq:wave_eq_int_xi}
\frac{\pd\phi}{\pd\eta}
=F(\eta)
\end{equation}
となり，もう一度積分すると，積分定数としてもう1つ関数が表れ
\begin{equation}
\label{eq:general_sol_form_wave_eq}
\phi
= f_1(\xi)+f_2(\eta)
\end{equation}
を得る。
(\ref{eq:wave_eq_int_xi})の代わりに$\eta$で積分しても，もちろん同様の結果が得られる。
いわばこの手順は，$\phi$に作用する2階の微分演算子を(\ref{eq:decompose_wave_eq_operator})の1行目のように因数分解し，それぞれ
\begin{equation}
\frac{\pd}{\pd\eta}
=
\frac{1}{2}
\left(\frac{\pd}{\pd x}
+\frac{1}{c}\frac{\pd}{\pd t}\right)
f_1(\xi)=0
\end{equation}
\begin{equation}
\frac{\pd}{\pd\xi}
=
\frac{1}{2}
\left(\frac{\pd}{\pd x}
-\frac{1}{c}\frac{\pd}{\pd t}\right)
f_2(\eta)=0
\end{equation}
を満たす解を重ね合わせた形である。
こうして，波動方程式の一般解の形が(\ref{eq:general_sol_form_wave_eq})のように決められる。
続いて，$f_1$と$f_2$それぞれの性質を調べるために，$f_2=0$の場合，すなわち$\phi=f_1(\xi)=f_1(x-ct)$の場合を考える。
$x$を固定すると，この関数は時間$t$とともに変化する。
また，$\xi=x-ct$が同じ値を取る$x$と$t$の組み合わせは無数にあり，同じ$\xi$の値を与える位置$x$および時刻$t$において，関数$f_1$は同じ値を持つ。
よって，ある位置$x_0$での時刻$t=0$における関数の値を
\begin{equation}
g \equiv f(x_0)
\end{equation}
とすると，時刻$t$後には，$x_0+ct$の位置において，$f(\xi)$の値が$g$となる。
なぜなら
\begin{equation}
f(\xi)=f(x_0+ct-ct)=f(x_0)=g
\end{equation}
したがって，$f_1(x-ct)$は，$x$の正の方向に，速さ$c$で伝播する波を表している。
同様の考察より，$f_2(x+ct)$は，逆方向に伝播する波を表すことが分かる。
よって$f_1(x-ct)$，$f_2(x+ct)$はそれぞれ，右向きおよび左向きの（あるいは正の向きの，負の向きの）進行平面波（traveling plane wave）と呼ばれる。
平面波は，波が同じ位相を持つ面，すなわち波面（wavefront）が，進行方向に垂直な平面になることからそう呼ばれる。
今考えている1次元の波は，3次元空間内を$x$方向に伝播しているものだとすると，$x$と$t$を固定してみたとき，関数$f_1$あるいは$f_2$の値は，$x=$一定で定められる面，すなわち$yz$平面内のどこでも同じであることがわかるだろう。
波面が平面でない波は後に扱う。
正弦波解
右向きに進行する波を考える。
固定された点で単振動をする波であるなら，解は
\begin{equation}
\phi(x,t)
= a\cos
\frac{2\pi}{\lambda}(ct - x)
\end{equation}
と置けるはずである。
ここで
\begin{equation}
\lambda
= \frac{2\pi c}{\omega}
\end{equation}
は波長（wavelength）である。
時刻$t$を固定すると，$x$が$\lambda$だけずれるとごとに位相が$2\pi$変化するから，$\phi$は三角関数の周期性から同じ値を取る。
他方，位置$x$を固定すれば，調和振動子の解と一致する。
$x=0$とすると
\begin{equation}
\phi(t)
= a\cos
\frac{2\pi c}{\lambda}
= a\cos(\omega t)
\end{equation}
の通りである。
時間$T=2\pi/\omega$だけずれると位相が$2\pi$変化して$\phi$は元の値に戻るから
\begin{equation}
T = \frac{2\pi}{\omega}
\end{equation}
は波の周期（period）を表している。
周期の逆数
\begin{equation}
\nu = \frac{1}{T}
\end{equation}
は振動数（frequency），あるいは周波数と呼ばれるが，波動の問題においては，角振動数$\omega$の方を単に振動数や周波数と呼ぶことが多い。
また，波数（wavenumber）
\begin{equation}
k
=\frac{2\pi}{\lambda}
\end{equation}
を導入すれば
\begin{equation}
\phi(x,t)
= a\cos(kx - \omega t)
\end{equation}
とも表現できる（$\cos\theta=\cos(-\theta)$）。
複素数を用いるなら
\begin{equation}
\label{eq:wave_solution_exp}
\phi(x,t)
=\Re{Ae^{i(kx-\omega t)}}
\end{equation}
である。
$\Re$は実部を取ることを意味する。
これが最もスタンダードな表現だろう。
分散関係と位相速度
波数と周波数は
\begin{equation}
\label{eq:dispersion_relation}
\omega^2
= c^2k^2
\end{equation}
の関係にある。
このような，波数と周波数の関係を分散関係（dispersion relation）と呼ぶ。
そして
\begin{equation}
c=\frac{\omega}{k}
\end{equation}
で与えられる波の速度を，位相速度（phase velocity）という。
位相速度自体が波数に依存しうるため，周波数はいつも単純に波数に比例するわけではない。
その場合，波は分散的（dispersive）であるという。
これまで，波の伝播方向を$x$軸にとり，1次元の空間で問題を考えてきたが，任意の座標系で記述できるよう表現を一般化する。
そのためには，位相速度の方向に単位ベクトル$\hat{\bm{n}}$を取り，波数を波数ベクトル（wavenumber vector）
\begin{equation}
\bm{k}
=\frac{2\pi}{\lambda}\hat{\bm{n}}
\end{equation}
に置き換える。
これにより，(\ref{eq:wave_solution_exp})は
\begin{equation}
\label{eq:wave_solution_exp_3D}
\phi(\bm{x},t)
=\Re{Ae^{i(\bm{k}\cdot\bm{x}-\omega t)}}
\end{equation}
と書き換えられる。
分散関係や位相速度の定義は，$k^2=k_x^2+k_y^2+k_z^2$によりそのまま成り立つ。
よって，容易に確かめられるよう，(\ref{eq:wave_solution_exp_3D})が満たす波動方程式は，3次元に一般化された
\begin{equation}
\nabla^2 \phi
-\frac{1}{c^2}\frac{\pd^2\phi}{\pd t^2}
=0
\end{equation}
である。
正弦波解(\ref{eq:wave_solution_exp_3D})が重要なのは，任意の波は，様々な波数$\bm{k}$を持つ正弦波の重ね合わせの形
\begin{equation}
\label{eq:wave_spectrum_decomposition}
\phi(\bm{x},t)
=\sum_{\bm{k}}
\Re{\phi_{\bm{k}} e^{i(\bm{k}\cdot\bm{x}-\omega t)}}
\end{equation}
によって表せるためである。
参考文献
- Landau, L. D., & Lifshitz, E. M. (1976). Mechanics 3rd ed. (Course of Theoretical Physics). Elsevier Science.
――(1986). 力学 (ランダウ=リフシッツ理論物理学教程). 広重 徹, 水戸 巌 訳. 東京図書.
- Landau, L. D., & Lifshitz, E. M. (1959). Fluid Mechanics: Landau and Lifshitz: Course of Theoretical Physics, Volume 6. 3rd Revised English ed. Pergamon Press.
――(1970). 流体力学 (ランダウ=リフシッツ理論物理学教程). 竹内均訳. 東京図書.
- Landau, L. D., & Lifshitz, E. M. (1975). The Classical Theory of Fields: Landau and Lifshitz: Course of Theoretical Physics, Volume 2. 3rd Revised English ed. (6th Russian ed.). Pergamon Press.
――(1978). 場の古典論（原書第６版） (ランダウ=リフシッツ理論物理学教程). 恒藤敏彦 & 広重訳. 東京図書.
- 山本 義隆 & 中村 孔一. (1998). 解析力学I&II. 朝倉書店.
- 米谷 民明. (1993). 力学. 培風館.
