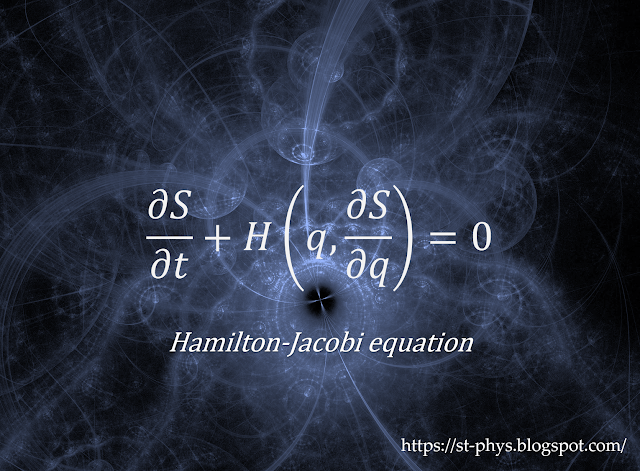Hamilton-Jacobi方程式の導出
作用を終点の時刻$t$と終点の位置$q$の関数とし,途中の時間パラメータを$t'$とすれば
\begin{equation}
S(q,t)=\int_{t_1}^{t_2} L(q(t'),\dot{q}(t'))dt'
\end{equation}
である。
まず,終点の空間的な位置はそのままで,そこに至る時刻がわずかに異なる軌道にずれた場合の作用の変化を考えよう。
元の物理的(physical)な軌道$q_p(t)$に対して,$\delta t$長く時間をかけて同じ点に至る非物理的(non-physical)な軌道を$q_{np}(t)$と記す。
時刻$t$においてこの軌道は,元の軌道からのずれで考えると
\begin{equation}
\label{eq:q_delta_t_diff}
q_{np}(t)=q_p(t)+\delta q(t)
\end{equation}
と書ける。
この軌道は終点で$q_{np}(t_2+\delta t)=q_p(t_2+\delta t)+\delta q(t_2+\delta t)$となるが,右辺1項目は$q_p(t_2+\delta t)=q_p(t_2)+\dot{q}_p(t) \delta t$と展開できるので,新たな軌道の終点は
\begin{equation}
q_{np}(t_2+\delta t)=q_p(t_2)+\dot{q}_p(t_2) \delta t + \delta q(t_2+\delta t)
\end{equation}
と書ける。
これが,元の軌道の終点$q_p(t_2)$と等しいため
\begin{align}
\label{eq:delta_q_qdot}
\delta q(t_2+\delta t)
=-\dot{q}_p(t_2) \delta t
\end{align}
が得られる。
終点をずらした新たな作用は
\begin{equation}
S_{np}
=\int_{t_1}^{t_2+\delta t}
L(q_{np}(t'),\dot{q}_{np}(t')) dt'
\end{equation}
である。
これに,(\ref{eq:q_delta_t_diff})を入れて展開すると
\begin{equation}
\label{eq:S_delta_t}
\begin{split}
S_{np}
=&
\int_{t_1}^{t_2+\delta t}
L(q_p(t'),\dot{q}_p(t')) dt' \\
&+
\int_{t_1}^{t_2+\delta t}
\left( \frac{\pd L_p}{\pd q} \delta q +\frac{\pd L_p}{\pd \dot{q}} \delta \dot{q} \right)
dt'
\end{split}
\end{equation}
となる。
ここで
\begin{equation}
L_p=L(q_p,\dot{q}_p)
\end{equation}
とした。
そして,2項目を部分積分することで
\begin{equation}
\label{eq:S_delta_t_ibp}
\begin{split}
S_{np}
=&
\int_{t_1}^{t_2+\delta t}
L(q_p(t'),\dot{q}_p(t')) dt' \\
&
+\left[\frac{\pd L_p}{\pd \dot{q}} \delta q \right]_{t_1}^{t_2+\delta t}
+\int_{t_1}^{t_2+\delta t} \delta q
\left( \frac{\pd L_p}{\pd q}
- \frac{d}{dt} \frac{\pd L_p}{\pd \dot{q}} \right) dt'
\end{split}
\end{equation}
を得る。
物理的に実現される軌道はEuler-Lagrange方程式を満たすから最後の項は消える。
また,(\ref{eq:S_delta_t})の右辺1項目の積分は,積分範囲を分けて
\begin{equation}
\label{eq:S_delta_t_1st}
\begin{split}
\int_{t_1}^{t_2+\delta t}
L(q_p(t'),\dot{q}_p(t')) dt'
=&
\int_{t_1}^{t_2} L(q_p(t'),\dot{q}_p(t')) dt' \\
&+\int_{t_2}^{t_2+\delta t} L(q_p(t'),\dot{q}_p(t')) dt' \\
=& S_p + L_p(t_2)\delta t
\end{split}
\end{equation}
とでき,残る表面項は先ほどの(\ref{eq:delta_q_qdot})の関係を用いると
\begin{equation}
\label{eq:S_delta_t_2nd}
\left[ \frac{\pd L_p}{\pd \dot{q}} \delta q \right]^{t+\delta t}
=-\left.\frac{\pd L_p}{\pd \dot{q}}\right|_{t_1}^{t_2+\delta t} \dot{q}_p(t_2) \delta t
=-p_p(t_2+\delta t) \dot{q}_p(t_2) \delta t
\end{equation}
となる。
ここで始点を固定していることより,下限での変分が消えることを使った。
まとめると
\begin{equation}
S_{np}
=S_p
+L_p\delta t
-p_p(t_2+\delta t) \dot{q}_p(t) \delta t
\end{equation}
である。
最後の項については$p_p(t_2+\delta t)\simeq p_p(t_2)+\dot{p}_p\delta t$とし,整理すると
\begin{equation}
S_{np}-S_p
=(L -p\dot{q} )_{t=t_2}\delta t
+O\left( (\delta t)^2 \right)
\end{equation}
となり,$\pd S/\pd t =\lim_{\delta t\to 0} (S_{np}-S_p)/\delta t$および$H=p\dot{q}-L $から結局
\begin{equation}
\label{eq:dSdt_H}
\left.\frac{\pd S}{\pd t}\right|_{t=t_2}
=(L-p\dot{q})_{t=t_2}
=-H(q(t_2),\dot{q}(t_2))
\end{equation}
にたどり着く。
添え字の$p$は省略した。
一方で,終点の空間的な位置がずれる場合,上と同様の計算から
\begin{equation}
\label{eq:delta_S_endpoint}
S_{np}
=\int_{t_1}^{t_2}
L(q_p(t'),\dot{q}_p(t')) dt'
+\left[\frac{\pd L_p}{\pd \dot{q}} \delta q \right]_{t_1}^{t_2}
+\int_{t_1}^{t_2}
\delta q
\left(\frac{\pd L_p}{\pd q}
- \frac{d}{dt}\frac{\pd L_p}{\pd \dot{q}} \right)dt'
\end{equation}
となり,改めてEuler-Lagrange方程式を用い,$\lim_{\delta q\to 0} (S_{np}-S_p)/\delta q$の極限を取ることで
\begin{equation}
\label{eq:dSdq_p}
\left.
\frac{\pd S}{\pd q}
\right|_{t=t_2} = p(t_2)
\end{equation}
を得る。
(\ref{eq:dSdt_H})と(\ref{eq:dSdq_p})を合わせて
\begin{equation}
\label{eq:dS_total_diff}
dS
=\sum_i p_i dq^i
-Hdt
\end{equation}
と書ける(添え字の$p$は省略した)。
また,(\ref{eq:dSdq_p})を(\ref{eq:dSdt_H})に入れることで
\begin{equation}
\frac{\pd S}{\pd t} +H\left(q, \frac{\pd S}{\pd q} \right) =0
\end{equation}
を得る。
これを,Hamilton-Jacobi方程式(Hamilton–Jacobi equation)と呼ぶ。
始点と終点の関数としての作用
上では,作用を終点の関数とみなしてその変分を考え,その結果,作用の全微分(\ref{eq:dS_total_diff})が得られた。
では,同様のやり方で始点を変化させた場合はどうなるか。
今度は積分の下限を変化させるため,(\ref{eq:dS_total_diff})と同じ形で符号が異なるものが得られるであろう。
実際に計算してみよう。
終点に至る時刻をずらした場合の計算(\ref{eq:S_delta_t_ibp})に対応するのは,始点での時刻$t_1$を$t_1+\delta t$にずらした場合の計算である。
(\ref{eq:S_delta_t_ibp})の右辺1項目の計算(\ref{eq:S_delta_t_1st})に対応するのは
\begin{equation}
\int_{t_1+\delta t}^{t_2}
Ldt
=
\int_{t_1}^{t_2} Ldt
-\int_{t_1}^{t_1+\delta t} L dt
=S_p-L_p\delta t
\end{equation}
であり,2項目の計算(\ref{eq:S_delta_t_2nd})に対応するのは
\begin{equation}
\left[ \frac{\pd L_p}{\pd \dot{q}} \delta q \right]_{t_1+\delta t}^{t_2}
=
\left.\frac{\pd L_p}{\pd \dot{q}}\right|_{t_1+\delta t} \dot{q}_p(t_1) \delta t
=p_p(t_1+\delta t) \dot{q}_p(t_1) \delta t
\end{equation}
であるから結局
\begin{equation}
\left.
\frac{\pd S}{\pd t}
\right|_{t=t_1}
=(p\dot{q}-L)_{t=t_1}
=H(q(t_1),p(t_1))
\end{equation}
となる。
始点の位置をずらした場合の計算も,(\ref{eq:delta_S_endpoint})において,今度は積分表面の下限を計算するに対応するから
\begin{equation}
\left.
\frac{\pd S}{\pd q}
\right|_{t=t_1}
= p(t_1)
\end{equation}
を得る。
したがって,始点$q_1=q(t_1)$の関数$S(q_1,t_1)$として見た場合の作用の変化は
\begin{equation}
dS
=-\sum_i p_idq^i+Hdt
\end{equation}
となり,望む結果が得られた。
そして,作用を始点と終点の関数$S(q_1,q_2,t_1,t_2)$として見た場合は,両点からの寄与を足し合わせ
\begin{equation}
dS
=(\sum_i p_idq^i -Hdt)_{t=t_2}
-(\sum_i p_idq^i -Hdt)_{t=t_1}
\end{equation}
となる。