三角関数

Keywords:

リンク

Introduction

三角関数の基礎について，物理をはじめとする数理科学への応用を念頭に解説する。ここでは高校の授業でやるような細かな話はしないが，逆に言えば，大半の数理科学分野の基礎を学ぶ上で必要な三角関数に関する基礎知識はそれほど多くなく，ここで扱う基礎さえ頭に入れておけば，必要な知識は，より具体的な内容を学んでいく過程で自然と発展させられるはずである。

三角関数の定義

$xy$平面に半径$r$の円を描き，原点$O$から円周上の点$P=(x,y)$を結ぶ線分$OP$と，$x$軸がなす角度を$\theta$とする（図1）。このとき，三角比（trigonometric ratio）は

\begin{equation} \label{eq:trigono_ratio} \sin{\theta}=\frac{y}{r}, \quad \cos{\theta}= \frac{x}{r}, \quad \tan{\theta} = \frac{y}{x} \end{equation}

で定義される。これを$\theta>90^\circ$の範囲にも一般化したものを，三角関数（trigonometric function）という。

三平方の定理より

\begin{align} r^2=x^2+y^2 \end{align}

であるから

\begin{align} \sin^2{\theta}+\cos^2{\theta}=1 \end{align}

が成り立つ。これはとても重要な関係だ。

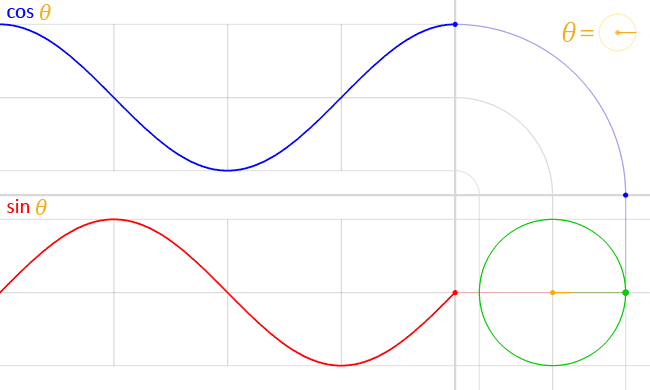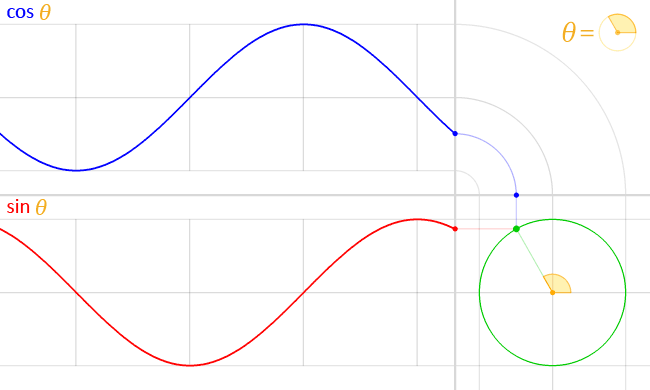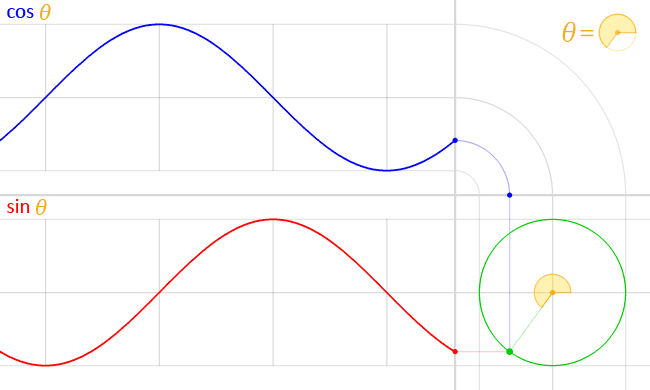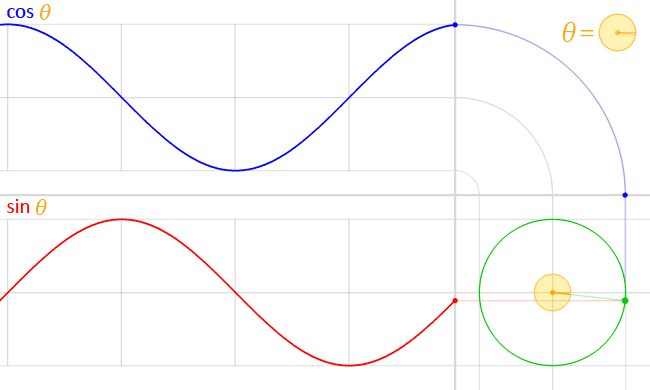
図１：半径$r$の円周上の点$P$の座標$(x,y)$と三角関数の関係

$\theta$にいくつか値を代入して具体的な値を確かめてみる。

$\theta=0$のとき，$x=r$および$y=0$であるため
\begin{align} \sin{0}=0, \quad \cos{0}= 1, \quad \tan{0} = 0 \end{align}
となる。
$\theta=\pi/2$のとき，$x=0$および$y=r$であるため
\begin{align} \sin{\frac{\pi}{2}}=1, \quad \cos{\frac{\pi}{2}}= 0, \quad \end{align}
となる。このとき，$\tan{(\pi/2)}$は分母が$0$になるため定義できない。
$\theta=\pi$のとき，$x=-r$および$y=0$であるため
\begin{align} \sin{\pi}=-0, \quad \cos{\pi}= -1, \quad \tan{0} = 0 \end{align}
となる。
$\theta=3\pi/2$のとき，$x=0$および$y=-r$であるため
\begin{align} \sin{\frac{3}{2}\pi}=-1, \quad \cos{\frac{3}{2}\pi}= 0, \quad \end{align}
となる。
そして，$\theta=2\pi$とすると，$\theta=0$の場合と同じ状態に戻る。

これらをグラフ化すると以下の図のようになる。

図2：三角関数のグラフ

ここで覚えておいてほしい重要なことは，$\sin{\theta}$および$\cos{\theta}$がとりうる値は$-1$から$1$であることだ。

原点付近での近似

$\sin{\theta}$のグラフの原点付近に注目すると，$\theta$が小さいとき，$\sin{\theta}$は傾き$1$の直線$y=\theta$とほぼ一致することがわかる（図3）。つまりこのとき

\begin{align} \label{eq:approx:sin} \sin{\theta} \simeq \theta \end{align}

という近似が成り立つ（$\simeq$は左辺を右辺で近似できることを表すことを示す記号）。

三角比(\ref{eq:trigono_ratio})に戻って考えると，$\theta$が0に近づくとき，三角形の高さ$y$は，円弧$r\theta$に近づくことがわかる。よって

\begin{equation} \sin\theta =\frac{y}{r} \simeq \frac{r\theta}{r} \end{equation}

であり，このことからも(\ref{eq:approx:sin})が得られる。この近似は非常によく用いられるものであるため，覚えておいてほしい。

図3：$\theta=0$付近での$y=\sin{\theta}$と，$y=\theta$のグラフ

$\cos{\theta}$については，$\theta=0$付近で

\begin{equation} \cos\theta = (1-\sin \theta^2)^{1/2} \simeq (1-\theta^2)^{1/2} \simeq 1-\frac{\theta^2}{2} \end{equation}

すなわち

\begin{align} \label {approx:cos} \cos{\theta} \simeq 1 -\frac{\theta^2}{2} \end{align}

が成り立つ（図4）。

図4：$\theta=0$付近での$y=\cos{\theta}$と，$y=1-\theta^2/2$のグラフ

加法定理

以下の式が成り立つことを，加法定理という。

\begin{align} \label{addsin} \sin(\alpha \pm \beta) = & \sin{\alpha}\cos{\beta} \pm \cos{\alpha}\sin{\beta} \\ \label{addcos} \cos(\alpha \pm \beta) = & \cos{\alpha}\cos{\beta} \mp \sin{\alpha}\sin{\beta} \\ \tan(\alpha \pm \beta) = & \frac{\tan{\alpha} \pm \tan{\beta} }{1\mp \tan{\alpha} \tan{\beta}} \end{align}

この関係は一般に余弦定理というものを使って導かれるが，以下の図を見て確認しておけば十分だ（必要だと思ったら今後導出法を書くかもしれない）。

図5：加法定理

三角関数の微分

最後に，三角関数の導関数を考える。図2を見ると，$\sin{\theta}$の傾きは，$\theta=0$で$1$，$\theta=\pi/2$で$0$，$\theta=\pi$で$-1$などとなっており，これをプロットしていくと$\cos{\theta}$のグラフと一致することがわかる。つまり

\begin{align} \notag \frac{d}{d\theta} \sin{\theta} = \cos{\theta} \end{align}

である。

$\cos{\theta}$の傾きについても同様に考えると

\begin{align} \notag \frac{d}{d\theta} \cos{\theta} =-\sin{\theta} \end{align}

となることがわかる。

このことを実際に計算で確かめよう。微分の定義に則って書き下すと$\sin{\theta}$の微分は

\begin{align} \label {def:dsin} \frac{d}{d\theta} \sin{\theta} = \lim_{\Delta \theta\to0} \frac{\sin(\theta+\Delta \theta) -\sin\theta }{\Delta \theta} \end{align}

となる。ここで$\sin(\theta+\Delta \theta)$に(\ref{addsin})を適用すると

\begin{align} \sin(\theta+\Delta \theta) = \sin{\theta}\cos{\Delta \theta} +\cos{\theta}\sin{\Delta \theta} \\ \end{align}

となる。これをまた(\ref{def:dsin})に戻してまとめると

\begin{align} \frac{d}{d\theta} \sin{\theta} = \lim_{\Delta \theta\to0} \frac{\sin{\theta}(\cos{\Delta \theta}-1) +\cos{\theta}\sin{\Delta \theta} }{\Delta \theta} \end{align}

となる。ここで$\Delta \theta\to 0$としてやれば，(\ref{approx:cos})より$\cos{\Delta \theta} \simeq 1 -(\Delta \theta)^2/2$であるから1項目が消える。残るのは

\begin{align} \frac{d}{d\theta} \sin{\theta} = \lim_{\Delta \theta\to0} \cos{\theta}\frac{\sin{\Delta \theta} }{\Delta \theta} \end{align}

であるが，$\Delta \theta\to 0$の極限では(\ref{eq:approx:sin})より$\sin{\Delta \theta}/\Delta \theta \to 1$となるため，最終的に

\begin{align} \frac{d}{d\theta} \sin{\theta} = \cos{\theta} \end{align}

が得られる。

同様に$\cos{\theta}$の微分

\begin{align} \label {def:dcos} \frac{d}{d\theta} \cos{\theta} = \lim_{\Delta \theta\to0} \frac{\cos(\theta+\Delta \theta) -\cos\theta }{\Delta \theta} \end{align}

については，(\ref{addcos})を用い

\begin{align} \frac{d}{d\theta} \cos{\theta} = \lim_{\Delta \theta\to0} \frac{\cos{\theta}(\cos{\Delta \theta}-1) -\sin{\theta}\sin{\Delta \theta} }{\Delta \theta} \end{align}

とし，あとは$\sin{\theta}$の場合と同様の極限操作により

\begin{align} \frac{d}{d\theta} \cos{\theta} =-\sin{\theta} \end{align}

が得られる。またこれらの結果を使うと

\begin{align} \frac{d^2}{d\theta^2} \sin{\theta} =& -\sin{\theta} \\ \frac{d^2}{d\theta^2} \cos{\theta} =& -\cos{\theta} \end{align}

という式も得られる。これらもまた物理をやる上で非常に重要になる。

$\tan{\theta}$の導関数については，$\sin{\theta}$および$\cos{\theta}$の結果をつかって

\begin{align} \frac{d}{d\theta} \tan{\theta} = \frac{d}{d\theta} \left( \sin{\theta}(\cos{\theta})^{-1} \right) \end{align}

を計算することで得られる。結果は

\begin{equation} \begin{split} \frac{d}{d\theta} \left( \sin{\theta} (\cos{\theta})^{-1} \right) =& \left( \frac{d}{d\theta} \sin{\theta} \right) (\cos{\theta})^{-1}+\sin{\theta}\frac{d}{d\theta}(\cos{\theta})^{-1} \\ =& \cos{\theta}(\cos{\theta})^{-1}-\sin{\theta}(\cos{\theta})^{-2}\frac{d}{d\theta}\cos{\theta} \\ =& 1 + \sin^2{\theta}(\cos{\theta})^{-2} \\ =& \frac{\cos^2{\theta}+\sin^2{\theta}}{\cos^2{\theta}} \\ =& \frac{1}{\cos^2{\theta}} \end{split} \end{equation}

である。