指数
指数の演算
$a$という数を2回かけ合わせたもの$a\times a$を$a^2$,3回かけ合わせたもの$a\times a\times a$を$a^3$と表す。これは,任意の自然数$n$について同じで,$a$を$n$回かけ合わせたものは$a^n$と表される。この$n$を指数という。
$m$と$n$を自然数とし,$a^m$と$a^n$をかけ合わせたものは,全部で$a$を$m+n$回かけあわせたものになるため
\begin{align}
a^m\times a^n=a^{m+n}
\end{align}
となる。
反対に,$a^m$を$a^n$で割ったものは,全部で$a$を$m-n$回かけ合わせたものになるため
\begin{align}
a^m\div a^n=a^{m-n}
\end{align}
である。
また,$a^m$を$n$回かけ合わせたもの,すなわち$(a^m)^n$は,$a$を$m\times n$回かけ合わせたものなので
\begin{align}
(a^m)^n=a^{mn}
\end{align}
となる。
このことは,$m$,$n$が自然数ではなく実数の場合も含め一般に成り立つ:
\begin{align}
\label {eqmn}
(a^m)^n=a^{mn}
\end{align}
この関係より,任意の数$a$の$0$乗は
\begin{align}
\label {zero}
a^0 = 1
\end{align}
と定義すると辻褄が合うことがわかる。
有理数べき乗
例えば$a^{1/2}$のような数は,2乗すると
\begin{align}
(a^{1/2})^2=a^{1}=a
\end{align}
となる。
このように,$1/2$乗した数を
\begin{align}
\sqrt a =a^{1/2}
\end{align}
と表し,$a$の平方根,あるいはルートと呼ぶ。
これを一般化し,任意の自然数$n,m=1,2,3,...$について
\begin{align}
^n \! \! \sqrt {a^m} =a^{m/n}
\end{align}
という表現をする。
対数
対数の演算
次に,$a$を何回かかけ合わせたら$x$になることがわかっていたとしよう。その何回かを$n$とすると,$a^n=x$である。これをひっくり返して,$n$に関する式として
\begin{align}
\log_a{x}=n
\end{align}
と表す。これが$\log$という記号の意味であり,この「何回か」を表す$n$を対数という。
このときの$a$を底というが,底がNapier数と呼ばれる特別な数$e$であるとき
\begin{align}
\log{x}=\log_e{x}
\end{align}
などと省略して書かれることが多い。ただ,底が$10$の時も同じ略記がされることもあるので,$e$を底としていることを明示するために$\ln{x}$という表記がされることもある。
最初の基本的な性質として,(\ref{zero})より,任意の$a$について
\begin{align}
\log_a{1}=0
\end{align}
が成り立つ。
次に,$a$を$m$回かけたものが$y$,すなわち$a^m=y$だったとすると,$a^m \times a^n=a^{m+n}$は$x\times y$となるから,これを対数の形にすると$\log_a{xy}=m+n$,すなわち
\begin{align}
\label {eq pls}
\log_a{xy}=\log_a{x}+\log_a{y}
\end{align}
となる。
他に重要な性質として(\ref{eq pls})と,その符号を反対にした場合の関係
\begin{align}
\label {x-y}
\log_a{\frac{x}{y}}=\log_a{x}-\log_a{y}
\end{align}
および(\ref{eqmn})より,正の数$x$と実数$t$について
\begin{align}
\label {lnxt}
\log_a{x^t}=t\log_a{x}
\end{align}
が成り立つ。
対数の実用的な例としては,例えば『Shannonの情報エントロピー』参照。
例題:
地震のエネルギーの規模を示す値,マグニチュード$M$は,地震により解放されるエネルギー$E$の対数を用いて
\begin{align}
\label{eq:magnitude}
\log_{10}E=1.5 M+4.8
\end{align}
と定義される。
$M$が$1$大きくなると$E$は約$32$倍,$M$が$2$大きくなると$E$は$1000$倍になることを計算により確かめよ。
ただし,$10^{0.5}\simeq 3.2$とする。
ちなみに,東日本大震災(2011)のマグニチュードは$9$,阪神大震災(1995)および熊本地震(2016)はマグニチュード$7.3$と推定される。
特殊な例
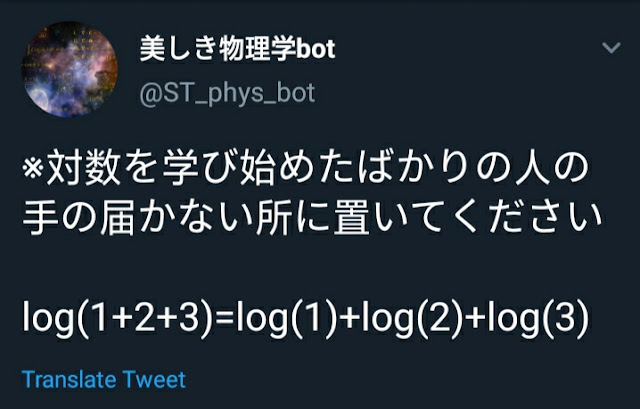
さて,これまでの説明からすると,トップ画像のような
\begin{align}
\label {abc}
\log{(a+b+c)}=\log{a}+\log{b}+\log{c}
\end{align}
という形の式は,一般に成り立たないことがわかる。しかし
\begin{align}
\label {123}
\log{(1+2+3)}=\log{1}+\log{2}+\log{3}
\end{align}
の例は間違った式ではない。それは,$1+2+3=1\cdot 2 \cdot 3=6$より,(\ref{eq pls})の等式が成り立つためである。
また,連続する自然数$n, n+1, n+2$について(\ref{abc})が成り立つのは,(\ref{123})の場合だけであることが示せる。
Euler数
微分の基本法則として,任意の自然数$n$について
\begin{align}
\frac{d}{dx}x^n =nx^{n-1}
\end{align}
が成り立つのであった。
ここで
\begin{align}
\label {def:e0}
f(x)= 1 + x + \frac{1}{2!}x^2 + \frac{1}{3!}x^3 +... = \sum_{n=0}^\infty \frac{x^n}{n!}
\end{align}
という関数を作って,その微分を考えてみる。
その前に馴染みない人のために記号の説明をしておくと,$n!$は$n$の階乗と呼ばれ,$n\cdot(n-1)\cdot(n-2)\cdot...\cdot 1$という演算を表している。
例えば$3!$であれば$3!=3\cdot 2\cdot 1=6$となる。
一番右の$ \sum_{n=0}^\infty$は,$n$に$0$から$\infty$まで代入したそれぞれの値を全部足し合わせることを示している。
こんな関数を作って何がありがたいかは,実際に微分してみるとわかる。
\begin{align}
\frac{d}{dx} f(x)
= \frac{d}{dx}1 +\frac{d}{dx} x + \frac{1}{2!}\frac{d}{dx}x^2 + \frac{1}{3!}\frac{d}{dx}x^3 +...
\end{align}
右辺1項目は定数の微分なので$0$,2項目は$1$,3項目は$2x/2!=x$,4項目は$3x^2/6=x/2...$となり,それぞれ微分する前に1つ前に並んでいた項に等しくなる。
これが無限に続くため,結局$f(x)$を$x$で微分した結果は
\begin{align}
\frac{d}{dx} f(x)
=1 + x + \frac{1}{2!}x^2 + \frac{1}{3!}x^3 +...=f(x)
\end{align}
となり,微分する前と変わらないことになる。
この関数は$f(x)$はある数の$x$乗$e^x$と等しいことが示される。
つまり
\begin{align}
e^x = \sum_{n=0}^\infty \frac{x^n}{n!}
\end{align}
である。
$e$は,$e^x$に$x=1$を代入したときの値
\begin{align}
\label {def:e1}
e=1+1+\frac{1}{2!}+\frac{1}{3!}+...=\sum_{n=0}^\infty \frac{1}{n!}
\end{align}
で,$2.71728...$という値に収束する。
これを,Euler数やNapier数と呼ぶ。
この数はまた
\begin{align}
\label {def:e2}
e=\lim_{n\to \infty} \left(1 + \frac{1}{n} \right)^n
\end{align}
あるいは$h=1/n$として
\begin{align}
\label {def:e3}
e=\lim_{h\to 0} \left(1 + h \right)^{1/h}
\end{align}
と表すこともできる。
(\ref{def:e2})が(\ref{def:e1})に一致することは,二項定理を使って$(1+1/n)^n$を実際に展開し,その後に$n\to \infty$の極限を取ることで確認できる。
指数・対数の微分
対数の微分
対数$y=\log_a {x}$の微分を定義通り考えると
\begin{equation}
\begin{split}
\frac{dy}{dx}
=& \lim_{\Delta x\to 0} \frac{\log_a {(x+\Delta x) - \log_a {x} }}{\Delta x} \\
=& \lim_{\Delta x\to 0} \frac{1}{\Delta x} \log_a { \left( \frac{x+\Delta x}{x} \right) } \\
=& \lim_{\Delta x\to 0} \frac{1}{\Delta x} \log_a { \left(1 + \frac{\Delta x}{x} \right) }
\end{split}
\end{equation}
となる。
2つ目の等式では(\ref{x-y})を使った。
ここで$h = \Delta x/x$とし,(\ref{def:e3})の定義を用いると
\begin{align}
\frac{dy}{dx}
=& \lim_{\Delta x\to 0} \frac{1}{h x} \log_a { \left(1 + h \right) } \notag \\
=& \frac{1}{x} \lim_{\Delta x\to 0} \log_a { \left(1 + h \right)^{1/h} } \notag \\
=& \frac{1}{x} \lim_{\Delta x\to 0} \log_a {e }
\end{align}
と変形できる。
上で説明した対数の基本的な関係を用いると
\begin{align}
\log_a {e}= \frac{\log_e{e}}{\log_e{a}}
\end{align}
を示せるため,最終的に
\begin{align}
\frac{d}{dx}\log_a {x} = \frac{1}{x \log_e {a}}
\end{align}
が得られる。
特に$a=e$のとき
\begin{align}
\frac{d}{dx} \log_e {x} = \frac{1}{x}
\end{align}
である。
$x < 0$の場合も同様の結果が得られるため
\begin{align}
\label {dlnx}
\frac{d}{dx} \log_e {|x|} = \frac{1}{x}
\end{align}
という公式が得られる。
$e^{ax}$の微分
続いて,$y=e^{x}$の導関数を求めるため
\begin{align}
\log_e {y} = \log_e { e^{x}}
\end{align}
の微分を考える。
左辺の$x$に関する微分は,(\ref{dlnx})とチェーンルールより
\begin{align}
\frac{d}{dx} \log_e {y} = \frac{1}{y} \frac{dy}{dx}
\end{align}
となる。
一方右辺は(\ref{lnxt})より
\begin{align}
\label {lnex}
\log_e { e^{x}} = x\log_e { e} =x
\end{align}
であるから,$x$で微分すると$1$になる。
左辺と右辺を結んで
\begin{align}
\frac{dy}{dx} = y
\end{align}
つまり,先に示した結果
\begin{align}
\frac{d}{dx} e^x = e^x
\end{align}
が得られる。
$x$によらない量$a$が含まれた$y=e^{ax}$の微分についても,(\ref{lnex})を
\begin{align}
\log_e { e^{ax}} = ax\log_e { e} =ax
\end{align}
と置き換えることで
\begin{align}
\frac{d}{dx} e^{ax} = ae^{ax}
\end{align}
となることがわかる。