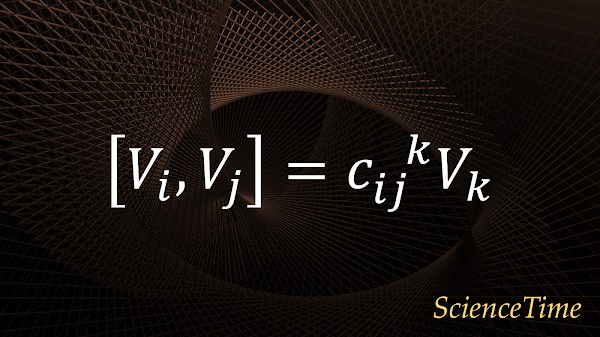内容

    1. ノート一覧
    2. 数学
    3. 微分幾何学

    Lie群のLie代数

    Dr. SSS 2021/02/28 - 14:53:54 1658 微分幾何学
    はじめに

    Lie群$G$は一般に複雑な構造を持った対象であるが，左移動という微分同相写像のために，その局所的な情報は単位元$e$の近傍に集約されている。 そのため，接空間を考えるにあたっても，$e$上の接空間$T_e G$が特別な重要性を持つ。 特に，Lie群の接空間はベクトル空間であるだけでなく，以下で定義する群のLie代数と呼ばれる構造を持っており，Lie群$G$の多くの情報がそこに含まれている。 このLie代数の構造もまた，$T_e G$上に課された構造とみなすことができ，これによりLie群全体の構造を分析するための効率的なアプローチが提供される。

    以下，$C^\infty$級多様体を念頭に議論するため，特に断りのない限り，多様体という言葉は$C^\infty$級多様体を指すものとする。 また，Einsteinの規約に従い，上下繰り返しの添え字は和を取ることとする（$\pd_i \equiv \pd/\pd x^i$は右辺の表現でも下付きとみなす）。


    keywords: Lie群, 一般線形群, 群論, Lie代数, 代数学, 微分幾何学, 線形Lie群, 多様体

    Lie代数

    Lie群$G$上の任意の不変ベクトル場$X,Y$は，任意の$a,b \in R$に対し

    \begin{align} \left. (aX+bY) \right|_g = \left.aX\right|_g +\left.bY\right|_g, \quad \forall g \in G \end{align}

    を満たす。 つまり，$G$上の不変ベクトル場全体の集合もまたベクトル場を構成する。 このベクトル場を$\mathfrak{g}$と記す。

    以下で示すように，$\mathfrak{g}$の任意の2元$X,Y\in \mathfrak{g}$からなるLie括弧$[X,Y]= XY-YX$は

    \begin{align} \label{eq:L_inv_Lie} L_{g*}[X,Y]_h=[X,Y]_{gh} \end{align}

    を満たすから，$[X,Y] \in \mathfrak{g}$であり，$\mathfrak{g}$はLie括弧に関して閉じている。 $\mathfrak{g}$とそのLie括弧$[\ ,\ ]:\mathfrak{g}\times \mathfrak{g} \to \mathfrak{g}$を合わせて，Lie群$G$のLie代数（Lie algebra）という。

    $\mathfrak{g}$の任意の元，つまり$G$上の不変ベクトル場$X$が与えられたとき，その$e$上での値$\left. X\right|_e$がわかれば

    \begin{align} \label{eq:LgXe} \left. X\right|_g=L_{g*}\left. X\right|_e \end{align}

    によって任意の点上の値もわかるから，左不変ベクトル場は$e$での値によって決定される。 反対に，$e$上の接空間$T_e G$の元$v$が与えられると，$L_{g*}v=X^v|_g$によって$\left.X^v\right|_e=v$となる左不変ベクトル場$X^v$を定義できる。 したがって，$\mathfrak{g}$と$T_e G$は1対1に対応付けられる。 これより，Lie代数の次元は，Lie群$G$の次元と一致する。

    この1対1対応があるため，Lie代数の構造を調べるにあたっても，$e$上での構造がわかればいい。


    構造定数

    単位元$e$上の接空間$T_e G$の基底を$\{V_i\}_{i=1}^n$とし，Lie括弧$[V_i,V_j]$を考えると，これも$T_eG$の元であるから，基底$\{V_i\}_{i=1}^n$を用いて

    \begin{align} \label{eq:Lie_VV} [V_i,V_j]=f_{ij}^{\ k}V_k \end{align}

    と表すことができる。 ここに現れる係数$f_{ij}^{\ k}$を構造定数（structure constants）という。 Lie群の群構造はこの構造定数によってほぼ決まる。 先に述べた事情から構造定数は$g$に独立な定数である。

    実際，基底$\{V_i\}_{i=1}^n$から左移動により各$g \in G$において$\left. X_i \right|_g = L_{g*}V_i$となる線形独立なベクトル場の組$\{X_i\}_{i=1}^n$が作れる。 そして，$[V_i,V_j]=[X_i,X_j]_e=f_{ij}^{\ k} \left. X_k \right|_e$であるから，(\ref{eq:Lie_VV})を左移動すると，(\ref{eq:LgXe})および(\ref{eq:L_inv_Lie})より

    \begin{align} L_{g*} [X_i,X_j]_e = [X_i,X_j]_g = f_{ij}^{\ k} \left. X_k \right|_g \end{align}

    となり，$f_{ij}^{\ k}$は$g$によらない定数でないといけないことが確認できる。


    式(\ref{eq:L_inv_Lie})の証明

    定義： 多様体$M$から$M'$への滑らかな（$C^\infty$級）写像$\varphi$があり，$M$上のベクトル場$X$と$M'$上のベクトル場$X'$が，任意の$p \in M$に関して

    \begin{align} \label{eq:phi_related} \varphi_* X_p =X'_{\varphi(p)} \end{align}

    を満たすとき，ベクトル場$X$と$X'$は$\varphi$-関係（$\varphi$-related）にあるという。


    補題： $M$上のベクトル場$X$と$M'$上のベクトル場$X'$が$\varphi$-関係にあるとき，$M'$上の滑らかな写像$f$と，任意の$p \in M$に対して

    \begin{align} \label{eq:phi-related_lemma} (X'f)\circ \varphi = X(f\circ \varphi) \end{align}

    が成り立つ。

    proof  

    1. $\varphi$-関係にあるという仮定より

      \begin{align} \varphi_*(X_p f) =X'_{\varphi(p)}f \end{align}

      である。

    2. 微分$\varphi_*$の定義と$X_p(f)=(Xf)(p)$より，左辺は

      \begin{align} X_p(f\circ\varphi) = (X(f\circ\varphi))(p) \end{align}

      右辺は

      \begin{align} (X'f)(\varphi(p)) = (X'f)\circ\varphi(p) \end{align}

      である。

    3. $p$は任意であるから，求める関係が得られる。
    □


    補題：$M$上のベクトル場$X,Y$と$M'$上のベクトル場$X',Y'$がそれぞれ互いに$\varphi$-関係にあるとき，Lie括弧$[X,Y]$と$[X',Y']$も$\varphi$-関係にある。

    proof  

    \begin{equation} \begin{split} [X',Y']_{\varphi(p)}f =& X'_{\varphi(p)}(Y'f)-Y'_{\varphi(p)}(X'f) \\ =& X_{p}((Y'f)\circ \varphi)-Y_{p}((X'f)\circ \varphi) \\ =& X_{p}(Y(f\circ \varphi))-Y_{p}(X(f\circ \varphi)) \\ =& [X,Y]_p (f\circ \varphi) \\ =& \varphi_*[X,Y]_p f \end{split} \end{equation}

    となり，求める結果が得られる。 最初と4つ目の等式はLie括弧の定義，2つ目の等式は$X'_{\varphi(p)}f=(\varphi_* X_p)f=X_p(f\circ \varphi)$，3つ目の等式は式(\ref{eq:phi-related_lemma})：$(X'f)\circ \varphi=X(f\circ \varphi)$，最後の等式は微分の定義を用いた。

    □

    さて，$L_{g*}X_e=X_g$より，左不変ベクトル場は左移動に関して(\ref{eq:phi_related})の関係を満たすから，上の補題より

    \begin{align} L_{g*}[X,Y] = [X,Y] \end{align}

    が成り立つ。 すなわち，左不変ベクトル場のLie括弧も左不変である。 こうして式(\ref{eq:L_inv_Lie})が示された。


    参考文献