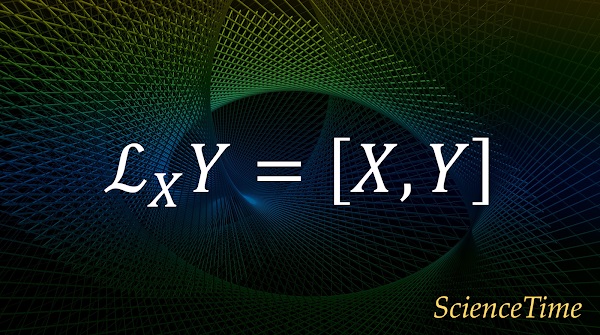Lie微分I：関数とベクトル場

Keywords:

リンク

Introduction

ベクトル場の積分曲線に沿った関数やベクトル場の変化率を求める操作を，Lie微分（Lie derivative）という。ここでは，関数とベクトル場のLie微分について説明する。

以下，$C^\infty$級多様体を念頭に議論するため，特に断りのない限り，多様体という言葉は$C^\infty$級多様体を指すものとする。また，Einsteinの規約に従い，上下繰り返しの添え字は和を取ることとする（$\pd_i \equiv \pd/\pd x^i$は右辺の表現でも下付きとみなす）。

関数のLie微分

ベクトル場$X$の積分曲線$c(t)$に沿った関数$f$のLie微分を考える。ベクトル場$X$によって生成されるフローを$\{\phi_t\}$とし，$p=c(0)$における関数の値と$\phi_t(p)=c(t)$における値を比較することで，積分曲線に沿った関数の変化を見ることができる。パラメータ幅$t$を無限小に取れば瞬間的な変化率が得られるから，$t=0$におけるベクトル場$X$の積分曲線に沿った関数$f$のLie微分は

\begin{align} \label{eq:Lie_deriv_f} \sL_X(f) = \lim_{t\to 0} \frac{\phi_t^* f -f}{t} \end{align}

と定義できる。ここで，右辺の$\phi_t^* f$は

\begin{align} \label{eq:phi_pullback} (\phi_t^* f)(p) \equiv (f\circ \phi_t)(p), \quad \forall p \in M \end{align}

で定義されている。 (\ref{eq:phi_pullback})の右辺は，点$\phi_t(p)$における$f$の値を表しているが，$f$を$\phi_t$によって「引き戻し（pull back）」して得られる合成関数$f\circ \phi_t$が点$p$における関数であることを明示するために，左辺のような特別な表記がなされている。

さて，すると点$p=c(0)$における関数$f$のLie微分は

\begin{align} \sL_X(f)(p) = \lim_{t\to 0} \frac{f(\phi_t(p))-f(p)}{t} = \lim_{t\to 0} \frac{f(c(t))-f(c(0))}{t} \end{align}

となる。これは，曲線$c$に沿った関数$f$の方向微分に他ならない。曲線に沿った変化率を考えているのだから，当然の結果である。よって，ベクトル場$X$で指定される$p$における接ベクトルを$X_p$とすると

\begin{align} \sL_X(f)(p) = X_p(f) =: (Xf)(p) \end{align}

という結果が得られる（最後の「$=:$」は右辺を左辺で定義するという意味）。 $p$は任意であるから結局

\begin{align} \sL_X(f) = Xf \end{align}

という公式が成り立つ。

微分

次に，ベクトル場のLie微分について考えるために，ベクトル空間の間の写像を定義する。

多様体$M$の点$p$を通る曲線

\begin{align} c:(-\varepsilon:\varepsilon) \to M, \quad c(0)=p \end{align}

を，微分同相写像$\phi$によって多様体$N$に写すと，$N$上の曲線

\begin{align} \phi\circ c:(-\varepsilon:\varepsilon) \to N, \quad \phi\circ c(0)=q \end{align}

が得られる。このとき，$p=c(0)$における接ベクトルを$q=\phi\circ c(p) $における接ベクトルに対応付ける写像を定義できる。これを

\begin{align} (d\phi)_p:T_pM \to T_qN \end{align}

または

\begin{align} \phi_*:T_pM \to T_qN \end{align}

と表し，点$p$における$\phi$の微分（differential）という。以下のベクトル場のLie微分における利用例のように，$M=N$でもいい。

$X$を$M$上のベクトル場とするとき，写像$\phi:M\to N$による微分により，$N$上のベクトル場

\begin{align} (\phi_* X)_{\phi(p)} \equiv (d\phi)_p(X_p) \end{align}

が得られる。これをある関数$f$に作用させた場合について考えると

\begin{align} \label{eq:diffX} (\phi_* X)_{\phi(p)}(f) = ((d\phi)_p(X_p))(f) = X_p(f\circ \phi) \end{align}

となる。

写像$\phi$とベクトル場$X$に関して次の有用な公式が成り立つ。

\begin{align} \label{eq:diff_prop} \phi^*(\phi_* X)f =X(\phi^* f) \end{align}

proof 点$p$でベクトル場$X$によって対応付けられるベクトルを$X_p$とする。点$p$における作用を考えると，(\ref{eq:diff_prop})の右辺はベクトル場と引き戻しの定義(\ref{eq:phi_pullback})より

\begin{equation} \begin{split} X(\phi^* f)(p) =& X(f\circ \phi)(p) \\ =& X_p(f\circ \phi) \\ \end{split} \end{equation}

である。次に，関係式(\ref{eq:diffX})と$(Xf)(p)\equiv X_p(f)$より

\begin{equation} \begin{split} X_p(f\circ \phi) =& (\phi_* X)_{\phi(p)}(f) \\ =& ((\phi_* X)f)(\phi(p)) \end{split} \end{equation}

であり，最後にまた引き戻しの定義(\ref{eq:phi_pullback})より，求める関係

\begin{equation} ((\phi_* X)f)(\phi(p)) = \phi^* ((\phi_* X)f)(p) \end{equation}

が得られる。

□

ベクトル場のLie微分

最後に，前の節の結果を利用して，ベクトル場$X$の積分曲線に沿ったベクトル場$Y$のLie微分を考える。

関数の場合同様に，ベクトル場の変化率を考えるためには，積分曲線上の異なる点におけるベクトルを比較する必要があるが，それぞれ異なるベクトル空間に属するベクトルをそのまま比較することはできない。そこで，ある点$p$におけるベクトル$Y_p$と，積分曲線に沿ってベクトル場を$t$逆戻しして定義されるベクトル場$(\phi_{-t})_*Y$の点$p$における値を比較する。この操作の無限小極限が，ベクトル場のLie微分

\begin{align} \sL_X(Y) f = \lim_{t\to 0} \frac{((\phi_{-t})_*Y)f -Yf } {t} \end{align}

である。関係(\ref{eq:diff_prop})を使うと，右辺の分子1項目は

\begin{align} ((\phi_{-t})_*Y)f =& ((\phi_{-t})^*)^{-1} \{Y((\phi_{-t})^* f)\} \notag \\ =& (\phi_{t})^* \{Y((\phi_{-t})^* f)\} \end{align}

と変形できる。 2つ目の等式で$(\phi_{-t})^{-1}=\phi_t$を使った。

これを代入し，$\lim_{t\to 0}[\{(\phi_t)^*(Yf)-(\phi_t)^*(Yf)\}/t]=0$を挿入すると

\begin{equation} \begin{split} \sL_X(Y) f =& \lim_{t\to 0} \frac{(\phi_{t})^*\{ Y((\phi_{-t})^* f)\} -Yf } {t} \\ =& \lim_{t\to 0} \left[ \frac{(\phi_{t})^*\{ Y((\phi_{-t})^* f) -Yf\} } {t} + \frac{(\phi_{t})^*(Yf)-Yf } {t} \right] \end{split} \end{equation}

となる。 1項目は

\begin{equation} \begin{split} \lim_{t\to 0} (\phi_{t})^* \frac{\{Y((\phi_{-t})^* f) -Yf\}}{t} =& \lim_{t\to 0} \frac{Y\{ (\phi_{-t})^*f -f\}}{t} \circ \phi_t \\ =& -Y(Xf) \end{split} \end{equation}

であり，2項目は$X$の積分曲線に沿った$Yf$の方向微分

\begin{align} \lim_{t\to 0} \frac{(\phi_{t})^*(Yf)-Yf } {t} = X(Yf) \end{align}

に他ならないから，結局

\begin{align} \sL_X(Y)f = [X,Y]f \end{align}

が得られる。ここで

\begin{align} [X,Y] \equiv XY-YX \end{align}

は，Lie括弧（Lie bracket）と呼ばれる。 $X=X^i \pd_i$および$Y=Y^i \pd_i$とすると

\begin{align} [X,Y] =& \left(X^i \frac{\pd}{\pd x^i} Y^j \frac{\pd}{\pd x^j} - Y^i \frac{\pd}{\pd x^i} X^j \frac{\pd}{\pd x^j} \right) \notag \\ =& \left(X^i \frac{\pd Y^j}{\pd x^i} - Y^i \frac{\pd X^j}{\pd x^i} \right)\frac{\pd}{\pd x^j} \end{align}

となり，$[X,Y]$もまた，$(X^i (\pd Y^j/\pd x^i)-Y^i(\pd X^j/\pd x^i))$を成分とするベクトル場となる。 $XY$や$YX$だけでは，2階微分が表れてしまい，ベクトル場にはならないことに注意しよう。