接ベクトルと接空間

Dr. SSS 2021/01/15 - 09:55:53 9848 微分幾何学

はじめに

ここでは，多様体の接ベクトルと接空間について説明する。以下，$C^\infty$級多様体を念頭に議論するため，特に断りのない限り，多様体という言葉は$C^\infty$級多様体を指すものとする。また，Einsteinの規約に従い，上下繰り返しの添え字は和を取ることとする（$\pd_i \equiv \pd/\pd x^i$は右辺の表現でも下付きとみなす）。

keywords: 位相空間, 接ベクトル, 接空間, 微分幾何学, 多様体

内容

多様体上の関数

多様体上の関数を考える。多様体$M$上の関数$f$とは，$M$の各点$p$に実数$f(p)$を対応付ける写像

\begin{align} f:M\to R ,\ p\in M \to f(p)\in R \end{align}

のことである。関数$f$は，任意の座標近傍$(U,\varphi)$に関する局所座標での表現

\begin{align} \label{eq:fU} f_U(x^1,...,x^n) =f\circ \varphi^{-1}(x^1,...,x^n) \end{align}

が局所座標$x^i$について微分可能であるとき，微分可能（differentiable）という。

ところで，$M$上の開集合$U$は$R^n$上の開集合$U'$と同相であるから，局所座標は$U$上に直に書き込まれているとみなしてしまっていい。すると，関数$f$を$f_U=f\circ \varphi^{-1}$と置き換える過程は省略し

\begin{align} \label{eq:f} f=f(x^1,...,x^n) \end{align}

のように，$f$を直接局所座標の関数として表現できる。

曲線と方向微分

曲線

多様体上の曲線も，数直線$R$から多様体への微分可能な写像として定義される。形式的に述べると

定義：$R$の開区間$(a,b)$から$C^r$級多様体$M$への$C^s$級写像$c: (a,b)\to M$を，$C^s$曲線という。ここで，$0 \leq s \leq r$である。

つまり，パラメータ$t\in (a,b)$の値に対応して，$M$上の点を指定するのが曲線だ。点$p$に対し，$c(t_0)=p$となる$t_0 \in (a,b)$が存在するとき，曲線$c$は点$p$を通るという。

$c$の像をまた，1対1写像$\varphi$によって$R^n$に写すことで，局所座標による表現

\begin{align} \label{eq:mapped-curve} \varphi(c(t)) =(x^1(t),x^2(t),...,x^n(t)) \end{align}

が得られるが，この場合もまた，$\varphi$によるマッピングを省略して$M$上の曲線と$\varphi$で写される$R^n$上の曲線(\ref{eq:mapped-curve})を同一視し，$c$を局所座標の関数として

\begin{align} c(t) = (x^1(t),x^2(t),...,x^n(t)) \end{align}

と表してしまって差し支えない。

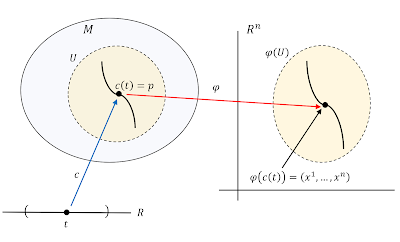
多様体$M$上の曲線のイメージ。

方向微分

$M$上で別の微分可能関数$f$を考えると，$f$は曲線$c$上の各点をある値に対応付ける：$f(c(t))\in R$。このような関数のパラメータ$t$に関する微分演算

\begin{align} \label{eq]dir_deriv} \left. \frac{df(c(t))}{dt} \right|_{t=t_0} = \lim_{\Delta t \to 0} \frac{1}{\Delta t} \left[f(c(t_0+\Delta t)) - f(c(t_0))\right] \end{align}

を，曲線$c$に沿った関数$f$の方向微分（directional derivative）という。

ここで

\begin{align} f\circ c = (f \circ \varphi^{-1}) \circ (\varphi \circ c) \end{align}

を使い，(\ref{eq:fU})，(\ref{eq:f})および(\ref{eq:mapped-curve})に注意すると，チェーンルールより

\begin{align} \left. \frac{df(c(t))}{dt} \right|_{t=t_0} = \left. \frac{df(x^1,...,x^n)}{dt} \right|_{t=t_0} = \left. \frac{dx^i}{dt} \right|_{t=t_0} \left(\frac{\pd f}{\pd x^i}\right)_p \end{align}

と表せる。

接空間

方向微分の対象となる微分可能関数$f$は任意であるから，方向微分の演算に注目し

\begin{align} \label{eq:v_p} \bm{v}_p \equiv \frac{dc}{dt} \equiv \frac{dx^i}{dt}\left(\frac{\pd}{\pd x^i}\right)_p \end{align}

と表現することにする。 $M$上のある点$p$を通る曲線は無数に考えられるから，$c(t)$とは別の曲線に沿った方向微分

\begin{align} \label{eq:u_p} \bm{u}_p =\frac{dx^i}{ds}\left(\frac{\pd}{\pd x^i}\right)_p \end{align}

を考え，(\ref{eq:v_p})と(\ref{eq:u_p})にそれぞれ定数$a,b$をかけて線形結合

\begin{align} \label{eq:tang_lin} a \bm{v}_p +b \bm{u}_p = \left(a\frac{\pd x^i}{\pd t } +b\frac{dx^i}{ds}\right) \left(\frac{\pd}{\pd x^i}\right)_p \end{align}

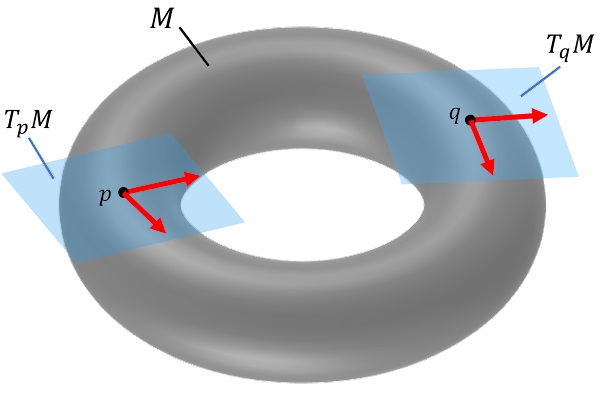
を作ると，これもまた点$p$を通る別の曲線に沿った変化を与える演算子となる。したがって，方向微分$\bm{v}_p$の集合は点$p$上で$\{(\pd/\pd x^i)_p\}$を基底とするベクトル空間を構成する（ベクトル空間であるための他の条件は直ちに確かめられる）。このベクトル空間を，点$p$における接ベクトル空間（tangent vector space）あるいは単に接空間（tangent space）といい，$T_pM$と表す。また，接空間の元を接ベクトル（tangent vector）という。

このとき，接ベクトルは多様体$M$ではなく，その接空間に属していること，そして，$M$上の異なる2点，$p,q$としよう，の上に定義される接空間$T_p M$と$T_q M$は互いに独立した空間であり，それらの元の間の演算はそのままでは定義できないことに注意しないといけない。

トーラスのような例では，トップの図のように，多様体に接した面としての接空間と，その中に横たわる矢印としての接ベクトルという視覚的イメージを与えることができる。

接ベクトルについてのコメント

$n$次元Euclid空間内の$n-1$次元（超）曲面上のベクトルは，$n$次元位置ベクトル$\bm{r}$の偏導関数

\begin{align} \label{eq:rbasis} \frac{\pd\bm{r}}{\pd x^i}, \quad (i=1,...,n-1) \end{align}

をベクトルの基底として展開される。例えば$R^3$内の単位球面$S^2$上の点は，3次元位置ベクトル

\begin{align} \bm{r} =\left( \begin{array}{c} \sin\theta \cos\phi \\ \sin\theta \sin\phi \\ \cos\theta \end{array} \right) \end{align}

によって指定され，接ベクトルの基底は

\begin{align} \bm{e}_\theta \equiv & \frac{\pd \bm{r}}{\pd \theta} = (\cos\theta \cos\phi, \cos\theta \sin\phi, -\sin\theta) \\ \bm{e}_\phi \equiv & \frac{\pd \bm{r}}{\pd \phi} = (-\sin\theta \sin\phi, \sin\theta \cos\phi, 0) \end{align}

で与えられる。このとき，基底ベクトルの長さが

\begin{align} \| \bm{e}_\theta \|=& 1 \\ \| \bm{e}_\phi \|=& |\sin\theta| \end{align}

と求まる。

これに対し，多様体の議論においては微分演算子$\{(\pd/\pd x^i)_p\}$が接ベクトルの基底に定められる。これについて，物理系の人ははじめ違和感を覚えることが多いが，これには重要な理由がある。

まず，多様体の定義には，多様体をその「外部」にあるより大きな空間に含まれているものと仮定するような要素は含まれていないため，(\ref{eq:rbasis})における$\bm{r}$のような高次元の量を仮定するわけにはいかない。また，一般の多様体には，計量などの付加的な構造を加えない限り，ベクトルの長さという概念が備わっていない。そのため，多様体に接するベクトルが，多様体の「外」に向かって突き出ているという描像を採用することはできないし，場合によっては長さという概念を与えることが意味をなさないこともある。

対して，$\{(\pd/\pd x^i)_p\}$は，高次元のベクトルやベクトルの長さといった概念によらないものであるため，考えている多様体の枠組み内で概念的に閉じているのである。こうした事情などから，微分演算子を基底とすることがより自然な選択となる。

参考文献

Frankel, T. (2011). The geometry of physics: an introduction. Cambridge university press.
Hawking, S. W., & Ellis, G. F. R. (1973). The large scale structure of space-time. Cambridge university press.
松本幸夫. (1988). 多様体の基礎. 東京大学出版会.
Nakahara, M. (2003). Geometry, topology and physics. CRC Press.
Schutz, B. F. (1980). Geometrical methods of mathematical physics. Cambridge university press
――(1987). 物理学における幾何学的方法. 家正則他訳. 物理学叢書
杉田勝実, 岡本良夫 & 関根松夫. (2007). 理論物理のための微分幾何学 - 可換幾何学から非可換幾何学へ. 森北出版
山本義隆 & 中村孔一. (1998). 解析力学I&II. 朝倉書店.