【微分幾何学】接バンドルとベクトル場および積分曲線

By ScienceTime Team Published on 2021-01-24 9 views
Header image

Yapparina, CC0, via Wikimedia Commons

Introduction

ここでは，多様体における接バンドル，ベクトル場そしてベクトル場の積分曲線といった概念について説明する。 以下，$C^\infty$級多様体を念頭に議論するため，特に断りのない限り，多様体という言葉は$C^\infty$級多様体を指すものとする。 また，Einsteinの規約に従い，上下繰り返しの添え字は和を取ることとする（$\pd_i \equiv \pd/\pd x^i$は右辺の表現でも下付きとみなす）。

多様体上の関数

多様体$M$上の接ベクトルをすべて集めたもの，すなわち接空間の和集合

\begin{align} TM \equiv \bigcup_{p\in M}T_p M \end{align}

も1つの多様体であり，接バンドル（tangent bundle）と呼ばれる。

接バンドル$TM$の元は接ベクトル$\bm{v}_p$であるから，多様体としての$TM$上の点は，$M$の点$p$と対応する接ベクトル$\bm{v}_p$の組$(p,\bm{v}_p)$で指定される。

点$p$を局所座標$(x^1,...,x^n)$，$\bm{v}_p$をその成分

\begin{align} v^i \equiv \frac{dx^i}{dt}, \quad (i=1,2,...,n) \end{align}

を使って表せば，接バンドル上の点は

\begin{align} (x^1,...,x^n, v^1,...,v^n) \end{align}

と馴染み深い表現によって表せる。 実際，質点の位置と速度で座標が指定される力学における状態空間は，微分幾何学の観点から見れば配位空間の接バンドルに他ならない。


ベクトル場と積分曲線

多様体$M$上の各点$p$に対して，接ベクトル$\bm{v}_p \in T_p M$を1つずつ対応付ける規則

\begin{align} X:M\to TM ,\ p\in M\to \bm{v}_p \in T_p M \end{align}

をベクトル場（vector field）という。 これについても，流体の速度場や電磁場のような純粋な物理的文脈で語られる例をイメージするといい。

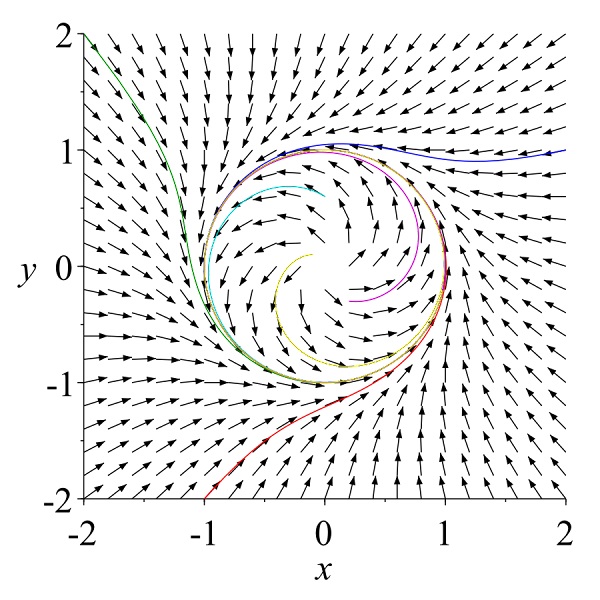
ある点からスタートし，ベクトル場$X$の規則に従って定まるベクトルに沿って点をつないで得られる曲線を，ベクトル場$X$の積分曲線（integral curve）という。 つまり，ある点における接ベクトルが，ベクトル場$X$によって指定されるベクトルと一致するということだから，積分曲線とは，曲線のパラメータ領域$(a,b)$に渡って

\begin{align} \label{eq:int_curve} \left. \frac{dc}{dt} \right|_t = X(c(t)) \end{align}

を満たす曲線$c$ということである。

(\ref{eq:int_curve})の左辺は，局所座標で表すと

\begin{align} \left. \frac{dc}{dt} \right|_t = \frac{dx^i(t)}{d t} \left( \frac{\pd}{\pd x^i} \right)_{c(t)} \end{align}

である。 他方，右辺のベクトルは

\begin{align} X(c(t)) = X^i(c(t)) \left( \frac{\pd}{\pd x^i} \right)_{c(t)} \end{align}

と表現できるから，(\ref{eq:int_curve})は

\begin{align} \frac{dx^i(t)}{dt} =X^i(x^1(t),...,x^n(t)), \quad (i=1,...,n) \end{align}

という$n$個の微分方程式として書き表せる。

References

  • Frankel, T. (2011). The geometry of physics: an introduction. Cambridge university press.
  • Hawking, S. W., & Ellis, G. F. R. (1973). The large scale structure of space-time. Cambridge university press.
  • 松本幸夫. (1988). 多様体の基礎. 東京大学出版会.
  • Nakahara, M. (2003). Geometry, topology and physics. CRC Press.
  • Schutz, B. F. (1980). Geometrical methods of mathematical physics. Cambridge university press
    ――(1987). 物理学における幾何学的方法. 家正則 他 訳. 物理学叢書
  • 杉田 勝実, 岡本 良夫 & 関根 松夫. (2007). 理論物理のための 微分幾何学 - 可換幾何学から非可換幾何学へ. 森北出版
  • 山本 義隆 & 中村 孔一. (1998). 解析力学I&II. 朝倉書店.

    • 接ベクトル
    • 微分幾何学
    • 微分方程式
    • ベクトル場
    • 多様体