Introduction
群の定義といくつかの基本概念を,具体例も用いて説明する。
群の定義
定義:
集合$G$が,以下の性質を満たすとき,$G$は群(group)であるという:
- 任意の$g_i, g_j \in G$について「積」$g_i\circ g_j$が定義され,$g_i \circ g_j$も$G$に属する。
- 任意の$g_i, g_j, g_k \in G$について$(g_i \circ g_j) \circ g_k=g_i \circ (g_j \circ g_k)$が成り立つ(結合則)。
- 単位元$e \in G$が存在し,任意の$g_i \in G$について,$e \circ g_i=g_i \circ e=g_i$が成り立つ。
- 任意の$g_i \in G$について,逆元$g_i^{-1} \in G$が存在し,$g_i \circ g_i^{-1}=g_i^{-1} \circ g_i=e$が成り立つ。
ある元$g_i, g_j$の間で$g_i\circ g_j=g_j\circ g_i$が成り立つとき,それらの元は互いに可換(commutative)であるという。 全ての元が可換である群を,可換群(commutative group)あるいはAbel群(Abelian group)といい,それ以外の群を非可換群あるいは非Abel群という。 Abel群の場合$g_i \circ g_j$に対応するものを$g_i +g_j$のように表記することも一般になされる。 いずれにしても,以下「$\circ$」は省略する。
$G$の部分集合$H$が,それ自身で群を成すとき,すなわち
- $a,b \in H$ならば$ab \in H$である。
- $a \in H$ならば$a^{-1} \in H$
であるとき,$H$を$G$の部分群(subgroup)という。
群の例
例1:対称群
ある集合$A$から$A$自身への写像を置換(permutation)という。 $A$を$n$個の元からなる有限集合とすると,$A$の各元$a_i \ (i=1,2,3,....n)$が置換によってそれぞれ$\sigma(a_i)$に移されることを
のように表す。 簡単な例として,$A=\{1,2,3\}$という集合を考えてみよう。 この集合の元に対して可能な置換は,それぞれ自分自身に置換するという操作も含めて
と全部で6通りある。
例えば$S_1$は $1 \to 2, \ 2 \to 3, \ 3 \to 1$ という置換を,$S_3$は $1 \to 1, \ 2 \to 3, \ 3 \to 2$ という置換を表しており,これらを$S_2 S_1$と続けて行った結果は $1 \to 3, \ 2 \to 2, \ 3 \to 1$ という置換を行うことに対応するから
という関係が成り立つ。 (\ref{eq:Sym})からなる集合を$G$とすると,同じようにして$G$の任意の元の積もまた$G$の元になり,かつ結合則も満たされることが確認できる。 また,$S_2S_1=e$より$S_1$と$S_2$は互いに逆の操作に,$S_3$から$S_5$はそれぞれ自分自身に対する逆の操作に対応しているから,この集合$G$は群をなすことがわかる。
この$G$の部分集合$H=\{e,S_1,S_2\}$もまた群である条件を満たすこと,すなわち部分群となっていることも確認できる。 一般に,$n$個の元を持つ集合上のすべての置換からなる集合は群を成し,$n$次の対称群(symmetric group)と呼ばれる
例2:2次元回転群
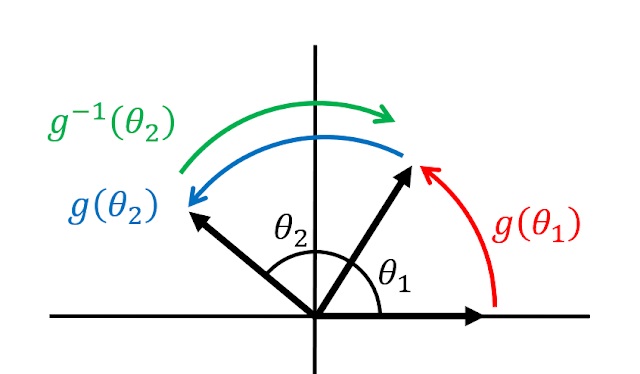
平面上の原点を中心にとする回転は,任意の2つの回転角を$\theta_1, \theta_2$とすると
という演算が成り立ち,結合則
も満たされる。 さらに,何もしないという操作が単位元に($g(0)=e$),任意の角度の回転に対して反対方向の操作が逆元に($g(-\theta)=g(\theta)^{-1}$)対応するため,この回転操作は群をなす(トップ画参照)。
平面上の点$\bm{x}=(x_1,x_2)$の回転は
と表せるから,2次元回転群は,2次元ベクトルに作用する行列
として「表現」することが出来る。 このとき,逆行列が逆元に,$R(\theta=0)$($=$単位行列)が単位元に対応している。