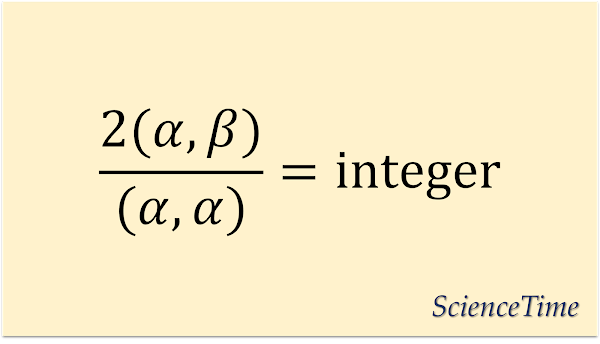ルートの性質

ここでは主にこれまでに示してこなかったルートおよび関連する概念の重要な性質を列挙し，後にそれらの証明を与える。 その前に1つ，以下で用いる概念を導入（おさらい）しておこう：

つまり，$X$の元のうち，$a \in A$だけを$Y$に写す写像$f(a)\in Y$のことである。 これを$f|_A$のように表す。

命題：重要な性質

1. 半単純Lie代数$\frg$の2つのルート$\alpha,\beta$に対し，$\alpha+\beta\neq 0$ならば$B(E_\alpha,E_\beta)=0$である。
2. 半単純Lie代数$\frg$のKilling形式を$\frh \subset \frg$に制限すると，Killing形式は非退化となる。
3. $\ad(E_\alpha),\ad(E_{-\alpha})$で不変な$V\subset \frg$に対し，$\tr(\ad(H_\alpha))$の$V$へ制限$\tr|_V (\ad(H_\alpha))$は0になる。
4. $\alpha\in \bigtriangleup$かつ，なんらかの整数$k$に対して$k\alpha\in \bigtriangleup$であれば，$k=\pm1$で$\dim\frg_\alpha=1$である。
5. 2つの異なるルート$\alpha,\beta$に対し，数
   \begin{align} N(\alpha,\beta) \equiv \frac{2(\alpha,\beta)}{(\alpha,\alpha)} \end{align}

   は整数になる。 この数は，Cartan整数（Cartan integer）と呼ばれる。

各命題の証明

1の証明

$E_\alpha \in \frg_\alpha, E_\beta \in \frg_\beta$および$E_\gamma \in \frg_\gamma$とすると，$\ad(E_\alpha)E_\gamma=[E_\alpha,E_\gamma]\in \frg_{\alpha+\gamma}$であるから，$\ad(E_\alpha):\frg_\gamma\to \frg_{\alpha+\gamma}$であり，同様に，$\ad(E_\alpha)\ad(E_\beta):\frg_\gamma\to \frg_{\alpha+\beta+\gamma}$である。 $\alpha+\beta \neq 0$であるから，すなわち$\ad(E_\alpha)\ad(E_\beta)$は$\frg_\gamma$を$\frg_\gamma$以外の空間に写す写像である。 よって$\ad(E_\alpha)\ad(E_\beta)$を行列表示すると，その対角成分は$0$になる。 よって，$B(E_\alpha,E_\beta)=\tr(\ad(E_\alpha)\ad(E_\beta))=0$である。

2の証明

$B$の$\frh$上への制限が非退化でないとすると，$\frg$上で非退化であるという事実に反するということを示す。

ある$H\in \frh$が，$\forall H' \in \frh$に対し

を満たすとする。 また，$\frh=\frg_0$であり$\forall\alpha \in \bigtriangleup$に対し$\alpha+0\neq 0$なので，命題1より$\forall E_\alpha \in \frg_\alpha$に対して

でもある。 $\frg$は$\frh=\frg_0$と$\frg_\alpha$の直和であるから，上の2つの式は，$\forall X \in \frg$に対し

であることを意味している。 $B$は$\frg$上で非退化であったから，$H=0$でないといけない。 よって，$B$の$\frh$上への制限も非退化である。

3の証明

$[E_\alpha,E_{-\alpha}]=H_\alpha$と$\ad([E_\alpha,E_{-\alpha}])=[\ad(E_\alpha),\ad(E_{-\alpha})]$および次元の等しい正方行列$A,B$に対して$\tr(AB)=\tr(BA)$が成り立つことから

となる。

4の証明

$[E_{\alpha},E_{-\alpha}]=H_\alpha$となる$E_\alpha\in \frg_\alpha$および$E_{-\alpha}\in \frg_{-\alpha}$を選ぶ。 また，ルートは有限であるから，$m\alpha$はルートだが，$(m+1)\alpha,(m+2)\alpha,...$はどれもルートではないような自然数$m$を取れる。 ここで$\frg$の部分空間

を用意する（$C$は複素数の集合）。 これは，$E_{-\alpha}$と$H_\alpha$および各$\frg_{k\alpha}$の元$E_{k\alpha}^{(1)},...,E_{k\alpha}^{(d_k)}$によって張られる空間である。 ここで$d_k=\dim \frg_{k\alpha}$とした。

この部分空間は $\ad(H_\alpha)$および$\ad(E_{\pm \alpha})$に対して不変だから

が成り立つ。

他方，$\ad(H_\alpha)E_{-\alpha}=-\alpha(H_\alpha)E_{-\alpha}=-(\alpha,\alpha)E_{-\alpha}$および，$\ad(H_\alpha)$の$\frg_{k\alpha}$上の固有値が$k\alpha(H_\alpha)=k(\alpha,\alpha)$であることから，$V$の元を

と並べたベクトルに作用する$\ad(H_\alpha)$の行列の部分は

の形になるため，(\ref{eq:trVHa})と合わせて

の関係が得られる。 これより，$d_1=1, d_2=d_3=...=0$とわかる。 同様のことを$\alpha \to -\alpha$として行うことで，命題が証明される。

5の証明

$\bigtriangleup$は有限集合なので，$k$を整数とすると有限個の$\beta+k\alpha$だけが$\bigtriangleup$に含まれる。 そこで，$-q\leq k \leq p$までは$\beta+k\alpha \in \bigtriangleup$だが，$\beta-(q+1)\alpha$も$\beta+(p+1)\alpha$はルートではないというように，整数$p,q\geq 0$が取れる。 これから$\frg$の部分空間

を取ると，$V$は$E_\alpha\in \frg_\alpha$および$E_{-\alpha}\in \frg_{-\alpha}$の随伴表現$\ad(E_\alpha),\ad(E_{-\alpha})$に対して不変であるから

となる。

他方，$\ad(H_\alpha)$の$\frg_{\beta+k\alpha}$上の固有値は

であるから，上の命題の証明と同様にして

と計算される。 (\ref{eq:trV0})および(\ref{eq:trV})より

が得られる。 $p,q$ともに整数であるから，この数は明らかに整数である。