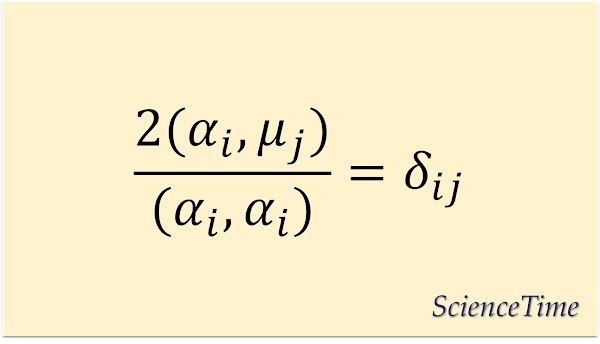【群論】最高ウェイトとウェイトの基本系

By ScienceTime Team Published on 2021-07-17 9 views
Header image

Introduction

半単純Lie代数の任意の表現は，既約表現の直和として得られる。 対して，半単純Lie代数の既約表現はLie代数の表現行列の固有値として与えられるウェイトの中で最大のもの，最高ウェイトにより一意に定められる。 ここでは，そのLie代数の表現のウェイトについて解説する。

最高ウェイト

ルートの場合と同様にしてウェイトに順序を入れたとき，ウェイトの集合の中で，順序が最大であるものを最高ウェイト（highest weight）という。

既約表現の最高ウェイトに縮退はなく対応する固有ベクトルは一意であり，最高ウェイトを共有する2つの表現は同値であることが言えるため，最高ウェイト$\mu$が定まったとすると，対応する状態$|\mu \rangle$に$E_{-\alpha}$を順次作用していくことで，既約表現のすべてのウェイトと対応する固有ベクトルを求め，既約表現を一意に決定することができる。


ウェイトの基本系

ウェイトも$\frh$の双対空間$\frh^*$の元であるから，何らかのルートの集合，例えばルートの基本系，からなる基底$\bm{e}^i=\alpha_i$によって

\begin{align} \label{eq:mu_mi1} \mu = \sum_{i=1}^l m_i \bm{e}^i \end{align}

と表すことができる。

しかし，ルートの基本系からCartan行列$C$の逆行列による線形変換で得られる

\begin{align} \left( \begin{array}{c} \mu_1 \\ \mu_2 \\ \vdots \\ \mu_l \end{array} \right) = C^{-1} \left( \begin{array}{c} \alpha_1 \\ \alpha_2 \\ \vdots \\ \alpha_l \end{array} \right) \end{align}

を基底に用いた方が都合がいい。 こうして与えられるウェイトの集まりをウェイトの基本系（fundamental system of weights）といい，その元を基本ウェイト（fundamental weight）という。

すると

\begin{align} \frac{2(\alpha_i,\mu_j)}{(\alpha_i,\alpha_i)} = (C^{-1})_{jk} \frac{2(\alpha_i,\alpha_k)}{(\alpha_i,\alpha_i)} = (C^{-1})_{jk}C_{ki} = \delta_{ij} \end{align}

が成り立つため，任意のウェイトをウェイトの基本系で

\begin{align} \label{eq:mu_mi} \mu=\sum_{i=1}^l m_i \mu_i \end{align}

と展開したとき

\begin{align} \frac{2(\alpha_i,\mu)}{(\alpha_i,\alpha_i)} = m_i \end{align}

という関係が得られる。

$\alpha_i$に関するウェイトの系列

\begin{align} \mu-q_i\alpha_i,\mu-(q_i-1)\alpha_i,...,\mu,...,\mu+(p_i-1)\alpha_i,\mu+p_i\alpha_i \end{align}

に対して

\begin{align} \label{eq:qpi} q_i-p_i = \frac{2(\alpha_i,\mu)}{(\alpha_i,\alpha_i)} \end{align}

が成り立つのであったから，すなわち$m_i=q_i-p_i=$整数である。 この$m_i$をDynkin indexという。


最高ウェイトである条件と基本表現

あるウェイト$\mu$が最高ウェイトであるのは，すべての単純ルート$\alpha_i$に対し，$\mu+\alpha_i$がウェイトではないときである。 これは(\ref{eq:qpi})において$p_i=0$であること，すなわち$m_i=q_i\geq 0$に対応する。 よって，ウェイト$\mu$が最高ウェイトであるのは，基本ウェイトで展開したとき，係数$m_i$がすべて0以上の整数である場合だといえる。

また，基本ウェイト$\mu_i$は，(\ref{eq:mu_mi})において，$i$番目の係数だけが1で，それ以外の係数をすべて0としたものであるものから，それ自身も最高ウェイトになる。 基本ウェイトを最高ウェイトとする表現を，基本表現（fundamental representation）という。


既約表現の次元

最高ウェイト$\mu$を持つ既約表現の次元$N$を与えるものとして，Weylの次元公式（Weyl dimension formula）

\begin{align} N=\frac{\prod_{\alpha>0} (\alpha,\delta+\mu)} {\prod_{\alpha>0} (\alpha,\delta)} \end{align}

が知られている。 ここで

\begin{align} \delta=\frac{1}{2}\sum_{\alpha>0}\alpha \end{align}

であり，積$\prod_{\alpha>0}$および和$\sum_{\alpha>0}$はすべての正ルートについて取る。


References

  • Arvanitogeōrgos, A. (2003). An Introduction to Lie groups and the Geometry of Homogeneous Spaces. American Mathematical Society.
  • Bincer, A. M. (2013). Lie Groups and Lie Algebras: A Physicist's Perspective. Oxford University Press.
  • Das, A., & Okubo, S. (2014). Lie Groups and Lie Algebras for Physicists. World Scientific.
  • Georgi, H. (2018). Lie Algebras in Particle Physics: From Isospin to Unified Theories. CRC Press.
  • Knapp, A. W. (1996). Lie groups beyond an introduction. Birkhäuser.
  • 佐藤 肇. (2000). リー代数入門: 線形代数の続編として. 裳華房.
  • 島和久. (1981). 連続群とその表現. 岩波書店.

    • Lie群
    • Lie代数
    • 固有値
    • 代数学
    • 固有値問題
    • 固有ベクトル
    • 対角化
    • 群の表現