集合とは

集合とは

素朴な見方では，「集合」という概念は日常的な感覚の通り，「ものの集まり」を指しており， 例えば「（既知の）動物種の集合」というと，我々ホモ・サピエンス（あるいはホモ・ペルニシオサス（Benatar 2015））を含めた動物種を集めたものになる。 Cantorも，集合という概念を次のように定義している。

集合とは，我々の直感や思考の対象となる明確に区別されたもの（objects）$m$を，一つにまとめたもの$M$のことであると理解する。

ある集合を構成する個々のものを，元または要素（element）と呼ぶ。 そして，ある元$x$が$A$に属しているということを，$x \in A$や$A\ni x$のように表す。 反対に，$x$が$A$に属さないことを$x \notin A$のように表す。 集合はもの（objects）の集まりとはいえ，その定義には単一の元から成る集合も含まれる。 このような集合をsingletonと呼ぶ。さらに，元を1つも含まないものも，集合とみなされる。 これを$\emptyset$で表し，空集合（empty set）と呼ぶ。

集合の表し方としては，その集合の元である条件$\varphi(x)$を用い

のように表す。 あるいは，元をそのまま羅列して

のように表すこともできる。

素朴な集合論の枠組みでは，任意の条件について，それ満たすものの集まりが集合として認められる。 これを無制限な内包公理，あるいはナイーブな内包原理などともいう（ナイーブではない内包公理はコチラで扱っている）。

日常的な場面では，メンバーが同じでも，異なる名前や役割の組織というのは存在するが，集合論的にはメンバーが同じ集合は同一のものとみなされる。 つまり，2つの集合$A$，$B$がまったく同じ元から成立っているとき，それらは等しい$(A=B)$という。これを外延性公理（axiom of extensionality）という。 このことを論理記号を使うと

と表せる。 ここで$\forall x$は「すべての$x$について」の意味で，その隣の括弧内の式が，$x$についての条件を示している。 矢印は，そのお尻の条件が真なら，その頭が指す先の条件も真であることを表す。 $\leftrightarrow$は双方についてその関係が成り立つことを示している。

部分集合と包含関係

集合$B$の元がすべて集合$A$にも含まれるとき，すなわち$x \in B$ならば$x\in A$が常に成り立つとき，$B$は$A$の部分集合（subset）と言い$B \subset A$や$A\supset B$で表す（図1）。 空集合や$A$自身もまた$A$の部分集合とみなされる。

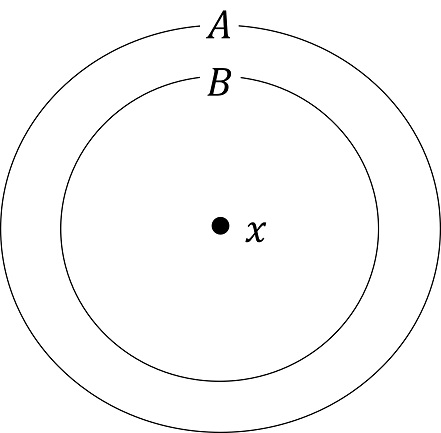
図1：$x\in B \subset A$の関係。

$A=B$であるというのは，すなわち$B \subset A$かつ$A \subset B$であるということである。 $\subset$や$=$で表される関係を包含関係（inclusion relation）という。

共通部分と和集合

$A$にも$B$にも属する元からなる集合を，$A$と$B$の共通部分（intersection）といい，$A\cap B$と表す。 「かつ（and）」に対応する論理記号$\land$を導入し，(\ref{eq:set_expression1})の記法を用いれば

である。 $A$か$B$，少なくともどちらかに属する元からなる集合を，$A$と$B$の和集合（union）といい，「または（or）」を表す記号$\lor$を導入すれば

と表される。

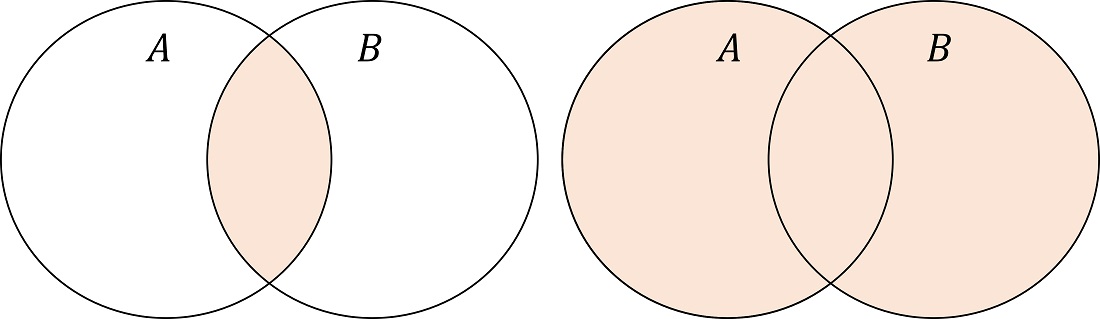
図2：$A\cap B$（左）および$A\cup B$（右）。

全体集合とDe Morganの法則

集合について考えるとき，対象を限定化して明確化するために，ある部分集合$U$に限って話を進めることが多い。 このときの$U$を，全体集合（universal set）という。 $U$の部分集合$A$に対し，$A$に属さない元からなる集合を，$A$の補集合（complement）といい，$\overline{A}$と表す（図3）。 すなわち

である。

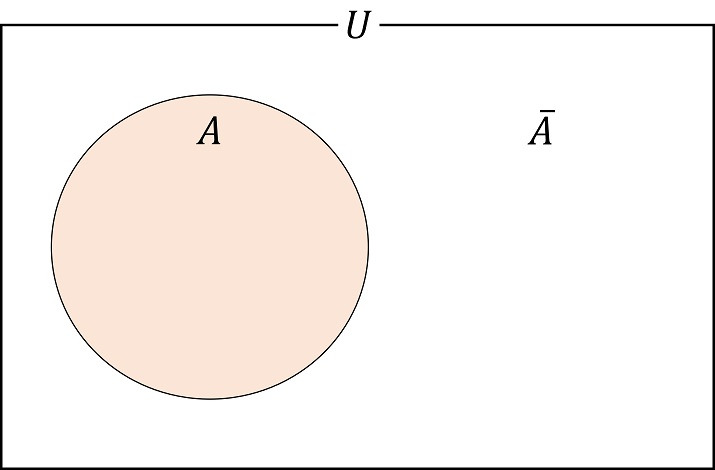
図3：$A$と$\overline{A}$。

De Morganの法則： 全体集合$U$およびその部分集合$A$および$B$について，次の関係が成り立つ：

\begin{align} \overline{A\cap B} =\overline{A}\cup \overline{B}, \quad \overline{A\cup B} =\overline{A}\cap \overline{B} \end{align}

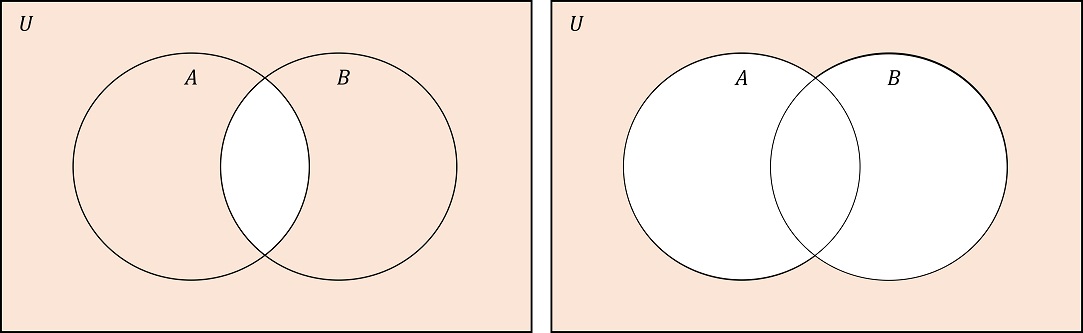
図4：$\overline{A\cap B} =\overline{A}\cup \overline{B}$（左）および $\overline{A\cup B} =\overline{A}\cap \overline{B}$（右）。