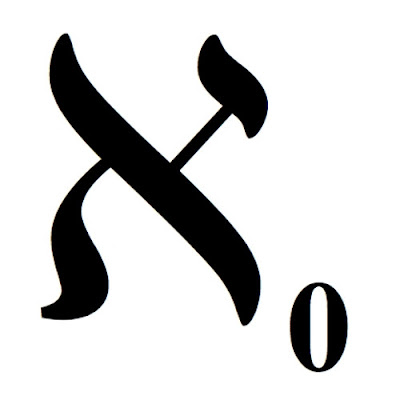可算集合の濃度

基数の概念を無限集合にも適用できるよう導入された，濃度という概念について説明する。

基数と序数

自然数には，物を$1, 2, 3, 4...$と数え，それらの物を，それぞれ自然数と対応させる，基数（cardinal number）としての機能と，物の一つ一つに番号を振って順序を付ける序数（ordinal number）としての機能がある。

わかりにくい場合は，例えば英語の表現one，two，three...とfirst，second，third...の違いを思い出せば区別が付けやすいかもしれない。

濃度

有限集合の基数は，その集合に含まれる要素を数え上げることで得られるが，例えば自然数全体の集合のような無限個の要素を持つ無限集合の場合には，すべての要素を数え上げるということはできない。しかし，ここで述べた基数の概念が無限集合にも適用できるよう，濃度（cardinality）という一般化された概念が導入される。

可算集合の濃度

2つの集合があり，それぞれの要素を互いに1対1に対応付けられるとき，それらの集合は同じ濃度を持つという。集合$M$の濃度は，$|M|$や${\rm card}(M)$などと表される。

自然数の集合$N$の要素と1対1に対応付けられる集合を，可算集合（countable set）という。そして，可算集合の濃度を$\aleph_0$で表す。$\aleph$の読みは「アレフ」で，$\aleph_0$は「アレフ・ゼロ」あるいは「アレフ・ヌル」と読む。

直和と濃度の和

互いに共通の元を持たない（共通部分が空：$A\cap B =\emptyset$）集合$A$と$B$の和集合を$A$と$B$の直和（disjoint union）といい，$A\sqcup B$と表す。 $A$と$B$が有限集合であれば，直和$A\sqcup B$の濃度は

と計算できる。 しかし，例えば$A$だけが有限集合で，$B$は可算集合であった場合，無限に有限の数を足しても無限であるため

となる。 $A$もまた可算集合である場合も

である。

可算集合の例

自然数の集合$N=\{1, 2, 3, 4...\}$の濃度を$\aleph_0$と定義したが，では自然数のうち，すべての偶数で構成される集合の濃度はどうなるだろうか？

$1, 2, 3, 4...$と並べていくと，偶数は1個おきにしか出てこないので，正の偶数の集合の要素は自然数全体の集合より少ないように思える。しかし同時に，この数字の羅列は無限に続くため，結局のところ正の偶数の集合も可算集合となる。実際，$N$の各要素を

という写像によって偶数の集合の要素と1対1に対応付けることができる。奇数についても同様である。つまりこれらの集合の濃度も$\aleph_0$である。

次に，整数の集合$Z=\{...-3,-2,-1,0,1,2,3,...\}$を考えてみる。この集合は負の数まで含むため，この集合もまた自然数の集合よりも大きな集合に思える。しかし濃度を比較すれば，これも可算集合であることがわかる。このことは

と偶数を正の整数に，奇数を0と負の整数に写すに写像によって，1対1に対応付けられることから確認できる。

無限の階層

これらの結果は反直観的であるが，無限は無限なので，そこでは大小関係などの概念も失われるのだろうか？

そうではない。

集合論の創始者であるCantorによって明かされた最初の興味深い事実こそ，無限には階層が存在しているということであり，この性質を調べる過程で，まだまだ多くの反直感的な事柄が示されていく。