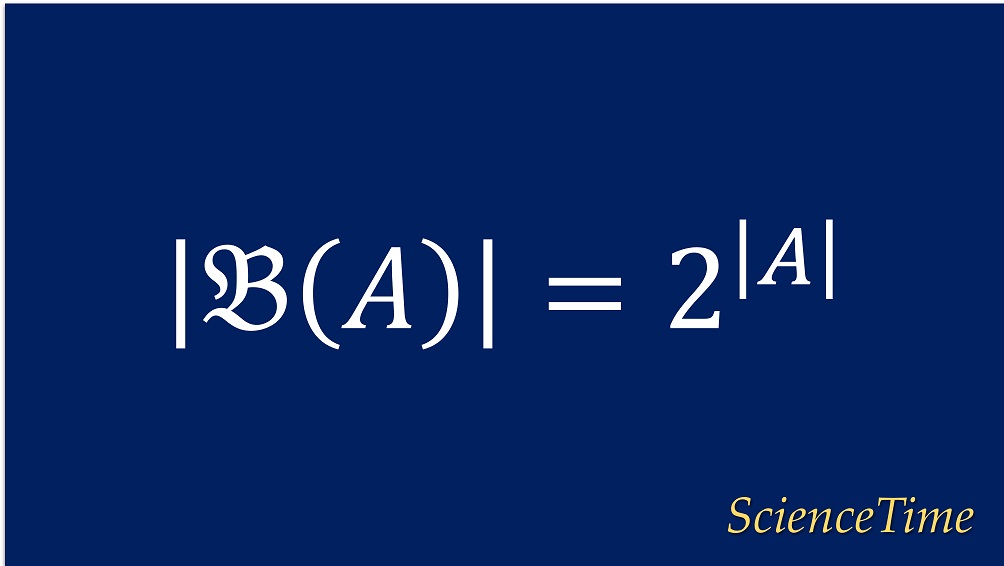部分集合とべき集合

部分集合とべき集合

集合$B$の元がすべて集合$A$にも含まれるとき，$B$は$A$の部分集合（subset）と言い$B \subset A$で表す。 空集合や$A$自身もまた$A$の部分集合とみなされる。 すると，例えば集合$A=\{ a, b, c \}$の部分集合は

となる。

また，集合$A$の8つの部分集合全体から成る集合

を$\mathfrak{B}(A)$と表し，$A$のべき集合（power set）と呼ぶ。

部分集合の個数とべき集合の濃度

一般に，$m$個の要素を持つ有限集合$A$の部分集合の個数は，$2^m$となる。 このことは以下のようにして示すことができる。 まず，引き続き$A=\{a,b,c \}$の例で考えよう。 $x \in A$の各要素がある集合$S$の要素であれば$1$，そうでなければ$0$を返す関数$f(x)$を考える。 集合$A$から部分集合を構成するというのは，$A$から特定の要素を選び出して，それ以外を捨てる操作に対応する。 そして，要素を選択することを$f(x)=1$，捨てることを$f(x)=0$と対応付けることができる。 つまり，(\ref{A_subset})においては

といった具合である。 対応付けの数は，各要素ごとに$0$か$1$の$2$通りずつあるため，$2\times 2\times 2=2^3$となる。 これを$m$個の要素を持つ集合のケースに一般化できることは明らかだろう。 よってまた，べき集合（power set）$\mathfrak{B}(A)$の濃度についての公式

が得られる。

自然数のべき集合の濃度

自然数の集合$N$についても式(\ref{eq:card_power_set})を適用することができ

となる。 また，この濃度は，連続体の濃度と等しい。 すなわち

である。 このことは以下のように示される。

区間$[0,1)$の実数の集合を考える。 2進数で表せば，$[0,1)$に含まれる任意の実数は，小数点以下の$0$と$1$の羅列で表現することができる。 そこで，例えば

なような要素を取り出したとき，小数点以下1桁目を$0$番目とし，$1$が現れる桁の番数を自然数に対応させることで

という集合を作ることができる。 これらはみな，自然数の集合の部分集合であり，すなわち自然数のべき集合の要素となっている。 このようにして，$[0,1)$の任意の要素に，自然数のべき集合の要素を1対1に対応付けられる。 『連続体の濃度：対角線論法と連続体仮説』での議論より，$[0,1)$の濃度も連続体の濃度$\aleph$を持つため，これより自然数のべき集合の濃度は，実数の濃度と等しいことがいえる。