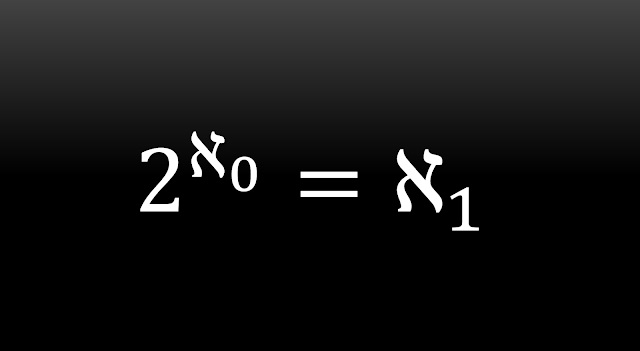【集合論】連続体の濃度：対角線論法と連続体仮説

By ScienceTime Team Published on 2020-06-10 4 views
Header image

Introduction

『可算集合の濃度』においては，自然数の集合の濃度について考えた。ここでは，自然数に続いて実数の集合について考えてみる。

実数とは

例えば数直線上の0と1に対応する点の間には，$0.1, 0.2, 0.3,...$といった小数で表される数に対応する点が限りなく存在している。 そして，0と0.1の間にも，$0.01, 0.02,...$と限りなく数が存在し$...$という確認の作業自体にも終わりはない。 このように，連続的な点の集まりから成る数直線上の点に対応する数を実数（real number）という。 結論から言うと，この実数をすべて集めて作られる集合$R$の濃度は$\aleph_0$ではない。

$R$の濃度が$\aleph_0$ではないということは，その各要素と自然数の集合$N$の要素との間に1対1の対応付けができないということである。 このことを示す方法の一つが，以下で解説するCantorの対角線論法（Cantor's diagonal argument）と呼ばれる論法を用いるものである。


対角線論法

まず，$0 < x < 1$を満たす数の集合を考え，それを$R(0,1)$と表そう。ちなみに，数直線上の区間$0 < x < 1$を$(0,1)$と表し，その端点（この場合$0$と$1$）が含まれない区間を開区間（open interval）という。他方，例えば$0\leq x \leq1$のように端点を含む区間を閉区間（closed interval）と言いい，$[0,1]$と表す。

さて，もし$R(0,1)$が可算集合であるとすると，それぞれの要素を自然数と対応付けて

\begin{align} R(0,1)=\{x_1, x_2,...,x_n,...\}, \ \ n \in N \end{align}

と並べることができる。この各要素を

\begin{equation} \label {diag} \begin{split} x_1 &= 0.a_{11} a_{12}...a_{1n}... \\ x_2 &= 0.a_{21} a_{22}...a_{2n}... \\ x_3 &= 0.a_{31} a_{32}...c_{3n}... \\ ...& \\ x_n &= 0.a_{n1} a_{n2}...a_{nn}... \\ ...& \end{split} \end{equation}

と無限小数に展開する。 そして

\begin{align} x' =0.b_1 b_2...b_n... \end{align}

という数を考える。 ここで，例えば$a_{nn}$が偶数なら$b_n=1$，奇数なら$b_n=2$とするなどして

\begin{align} b_1 &\neq a_{11} \notag \\ b_2 &\neq a_{22} \notag \\ b_3 &\neq a_{33} \label {bn} \\ ...& \notag \\ b_n &\neq a_{nn}... \notag \\ ...& \notag \end{align}

を満たすよう$x'$を決める。 するとこの$x'$は$x' \in R(0,1)$であるが，$x_1,x_2,...,x_n,...$のどれとも一致しない。 なぜなら，上で述べた$x'$の条件(\ref{bn})から，$x_1$とは小数点一桁目（$a_{11}$）が，その他任意の$n$について$x_n$とは$n$桁目（$a_{nn}$）が異なっているからである。 よって，$R(0,1)$を可算集合とする仮定と矛盾するため，$R(0,1)$は可算集合でなく，$R(0,1)$は$N$より大きな濃度を持っているということになる。

では，数直線上で，$(0,1)$というほんのわずかな区間に含まれる実数の集合ですら$N$より大きな集合であるということは，実数の集合$R$はさらに大きな濃度を持つのではないか，と思うかもしれない。 しかし，そこはそうではない。

\begin{align} \label {eq:tan_map} f(x) = \tan {\left\{\pi \left(x-\frac{1}{2}\right) \right\}} \end{align}

といった写像によってそれぞれ1対1の対応付けが出来るため，$R$と$R(0,1)$は同じ濃度を持っていることになる。

こうして，実数の集合の濃度は自然数の集合の濃度$\aleph_0$より大きいことがわかった。 この実数の集合と同じ濃度を持つとき，連続体の濃度$\aleph$を持つという。 $\aleph_0$と$\aleph$の存在により，無限の中にもある種の階層が存在することがわかった。 集合論の始まりは，1873年にCantorがこの階層を見出した時であると言われる。


連続体仮説

Cantorは，自然数の集合の濃度$\aleph_0$と連続体の濃度$\aleph$の間に他の濃度は存在しないこと，つまり，$\aleph_0$の次に大きな無限集合の濃度を$\aleph_1$と表したとき

\begin{align} \label {cont_hyp} \aleph = \aleph_1 \end{align}

が成り立つという仮説を提唱した。 これが連続体仮説（continuum hypothesis）と呼ばれるものである。 コチラで説明しているように，$\aleph=2^{\aleph_0}$が成り立つことが示せるため，(\ref{cont_hyp})は

\begin{align} \label {cont_hyp2} 2^{\aleph_0} = \aleph_1 \end{align}

とも表される。 また，(\ref{cont_hyp})の一般化である，任意の順序数$\alpha$について

\begin{align} 2^{\aleph_\alpha}= \aleph_{\alpha+1} \end{align}

が成り立つという主張は，一般連続体仮説と呼ばれる。 順序数についての説明は別記事で行う。

後に数学界では，集合論を厳密な公理系として整備する動きが起こり，ZFと呼ばれる公理系が一般に採用されるようになった。 現在では，連続体仮説はZF内部では証明も反証もできない（すなわちZFとは独立な）命題であることがわかっている。


  • 集合論
  • 連続体仮説
  • Georg Cantor
  • 数学