内容

    1. ノート一覧
    2. 数学
    3. 微分幾何学

    立体射影

    Dr. SSS 2021/08/20 - 09:54:28 6454 微分幾何学
    はじめに

    多様体は，チャート（開近傍とEuclid空間への写像の組）を張り合わせて構成されるが，複数のチャートを必要とするもののうち，最も単純で身近な例が球である。

    以下では，2次元単位球面$S^2$から北極$N=(0,0,1)$の1点を除いた$M=S^2-\{N\}$から$R^2$への同相写像（相互に連続な1対1写像）を定義する方法と，その写像の具体的な表現について説明する。


    keywords: 位相空間, 立体射影, 多様体

    立体射影

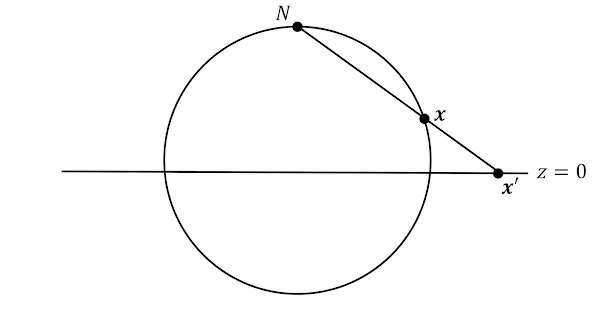
    $x^2+y^2+z^2=1$で定義される2次元単位球面$S^2$を考える。 単一の写像では，$S^2$を1対1でEuclid平面$R^2$に対応付けることはできないが，$S^2$から北極$N=(0,0,1)$の1点を除いた$M=S^2-\{N\}$から$R^2$であれば，次のようにして，同相写像を定義することができる。

    下図のように，$N=(0,0,1)$から$S^2$上の点$\bm{x}=(x,y,z)$を通る直線$l$を引き，$z=0$で定義される面$R^2$との交点を$\bm{x}'=\varphi(\bm{x})$とすると，この写像$\varphi$は同相になる。 これを，ステレオ投影（stereographic projection）や立体射影などという（トップの図はこの写像の断面図）。

    以下，この写像の具体的な表現を考える。


    立体射影の表現

    直線$l$は，パラメータ$t$を用いて

    \begin{align} \label{eq:StereoPara} t\bm{x}+(1-t)N = (tx,ty,tz+(1-t)) \end{align}

    と表すことができる。

    $\varphi(\bm{x})$における$t$の値$t_0$は，$z$座標を0として

    \begin{align} t_0z+(1-t_0)=0 \end{align}

    より

    \begin{align} t_0=\frac{1}{1-z} \end{align}

    と決まる（$\bm{x}\neq N$なので$z\neq 1$）。 これを(\ref{eq:StereoPara})に入れると

    \begin{align} \label{eq:phix} \varphi(\bm{x}) = \left( \frac{x}{1-z}, \frac{y}{1-z} \right) \end{align}

    が求まる。

    今度は反対に，平面$R^2$から$S^2$への写像の表現を求める。 $R^2$の点を$\bm{x}'=(x',y')$とすると，(\ref{eq:phix})より

    \begin{align} \label{eq:xyprime} x'=\frac{x}{1-z}, \quad y'=\frac{y}{1-z} \end{align}

    であるから，これと$x^2+y^2+z^2=1$の関係を合わせると

    \begin{align} \label{eq:1-z2x2} (1-z^2)|\bm{x}'|^2=1-z^2 \end{align}

    が得られ，$z\neq 1$であるから$(1-z)$で割ることができて

    \begin{align} (1-z)|\bm{x}'|^2=1+z \end{align}

    となる。

    これを整理することで，結果的に

    \begin{align} z=\frac{|\bm{x}'|^2-1}{|\bm{x}'|^2+1} \end{align}

    という関係が得られる。 これを(\ref{eq:xyprime})に入れることで$x',y'$の表現も得られる：

    \begin{align} \bm{x} =\varphi^{-1}(\bm{x}') = \left( \frac{2x'}{|\bm{x}'|^2+1}, \frac{2y'}{|\bm{x}'|^2+1}, \frac{|\bm{x}'|^2-1}{|\bm{x}'|^2+1} \right) \end{align}


    複素空間の場合

    応用的に重要になるため，$y$軸を虚軸とし，$z=0$の平面を複素平面とみなした場合の表現についても考えておこう。 このとき$\varphi$によって$\bm{x}\in M$は，複素平面上の1点に写されるから，(\ref{eq:phix})に対応するのは

    \begin{align} \varphi(\bm{x}) = \zeta\equiv \frac{x+iy}{1-z} \end{align}

    である。

    反対に複素平面上の点$\zeta$からの逆像は，(\ref{eq:1-z2x2})に対応する式が

    \begin{align} (1-z^2)|\zeta|^2=1-z^2 \end{align}

    となることから

    \begin{align} z=\frac{|\zeta|^2-1}{|\zeta|^2+1} \end{align}

    および

    \begin{align} \label{eq:cmplx_xy} x+iy= \frac{2\zeta}{|\zeta|^2+1} \end{align}

    となる。

    (\ref{eq:cmplx_xy})の複素共役を取り足し引きすることで，$x,y$個別の表現

    \begin{align} x= \frac{\zeta+\zeta^*}{|\zeta|^2+1}, \quad y= \frac{\zeta-\zeta^*}{i(|\zeta|^2+1)} \end{align}

    も得られる。


    参考文献