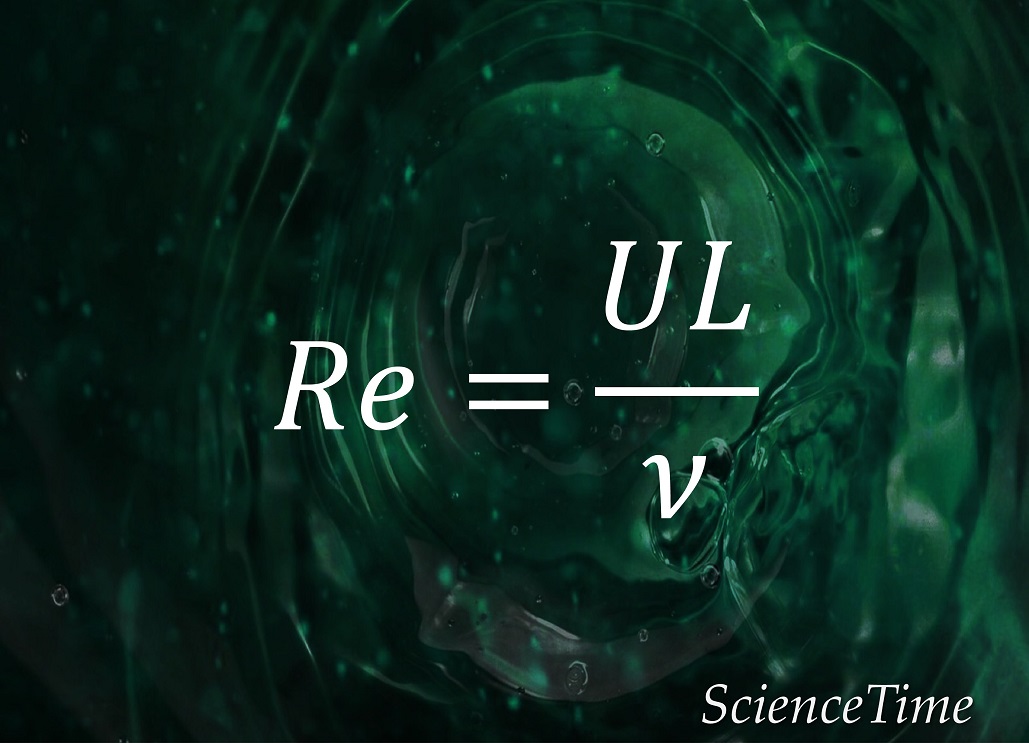Reynolds数と乱流

層流と乱流

流体の流れは，大きく分けて，層流（laminar flow）と乱流（turbulent flow）の2種類に分けられる。 簡単に言えば，層流は，渦も分断もない平行な層からなる流れで，乱流はそれと対照的に，流体の各要素が混ざり合う流れのことを言う。 多くの場合，層流は，十分ゆっくりか，小さなスケールでなければ維持できない。 例えば水道の水を見ても，蛇口を軽くひねってゆっくり流せば，流れは安定的であるのに対し，水量を増やして速くするほど，流れは不安定になって乱れることが観察できる。

まるで流れていないかのような綺麗な層流（laminar flow）

層流とは：https://t.co/zLWqfm6Cfl pic.twitter.com/fMMVQurZol

— 美しき物理学bot (@ST_phys_bot) April 21, 2023

乱気は自然に遍在しており，大きなスケールの現象でいうと，太陽から噴き出す紅炎（プロミネンス；prominence）と関連して起こる太陽フレアと呼ばれる爆発現象も，その発生源に乱流が関与した現象である。 フレアに伴うX線や高エネルギー粒子の放出は地球にも影響を及ぼすが，その影響から身を守る地球磁場も，惑星中心部の乱流対流を起源としている。 大気や海洋の流れにも様々な乱流が含まれているし，より身近な，燃焼プロセス，立ち上る煙や車の周りの空気の流れなど，乱流は様々な場面，スケールに見られる。

これらの乱流現象の理解を深めることは，実用上も大きな意味を持つ。 大気の乱流は，観測の障害となったり，気象予報を困難なものにしたりするし，航空機の安全性や効率にもかかわる。 周囲の乱流を制御するという点では，車の設計においても同様の知識と技術が要求される。

NASAのソーラー・ダイナミクス・オブザーバトリー（SDO）が捉えた紅炎爆発 pic.twitter.com/l5gdN3pcSd

— 美しき物理学bot (@ST_phys_bot) December 1, 2019

乱流の理論

では，乱流を理解し，その振る舞いを予測するためにどのようなアプローチが可能であるだろうか。 その不規則で乱雑な性格から，時々刻々とした速度場の状態を正確に予測することは困難であろう。 それでも，統計的なアプローチによって，何らかの一般的な法則性が抽出できるのではないだろうか。

しかし，統計的な方程式は，常に方程式の数より未知数が多くなり方程式系が閉じない，いわゆるclosure問題を抱えており，方程式と未知数の数を揃えるために，しばしばアドホックな仮定が用いられる。 そして，エネルギースペクトルのKolmogorov則などの極少数の例を除いて，普遍的な法則というものは見出されていない。 現実には，境界層や磁気流体など，それぞれ特定の対象のみに適用可能な理論がいくつもあるだけで，それらを束ね，乱流という現象を統一的に扱える形式的な理論は存在していない。 そのような形式的な乱流の理論を構築できるという見込みがあるのかすらわからないのである。

乱流の特徴

そもそも乱流という物理概念に簡潔な定義を与えることからして困難である。 だが，その代わりに乱流とみなされるものに共通する基本的な性質を羅列することはできる。

いくつかの文献（参考文献参照）を参考に代表的なものを羅列すると

• 予測不能性：わずかな初期条件の違いにより，速度場のその後の時間発展が大きく変わるという意味で，予測不能である。
• 不規則性：速度場が時間的にも空間的にも非常に不規則な構造を持つ。
• 散逸性：粘性による散逸を補うエネルギー供給がなければ，乱流は減衰してやがて消滅してしまう。 言い換えると，乱流が維持される系は，その外部からエネルギー供給を受けている開放系，すなわち散逸系である。

などが挙げられる。 他にも，流体として扱っている以上，最小のスケールでも分子スケールに比べれば十分大きく，連続体近似が成り立つなどの条件は当然仮定されている。 これらの性質に対応する数学的性質や応用上の影響などは具体的な例を扱う中で見ていくことにしよう。

Reynoldsの実験

層流と乱流を明確に区別し，それらの状態間の遷移に関して最初の重要な洞察を与えたのは，Osborne Reynolds (1883) である。 彼は滑らかでまっすぐなパイプに着色した水を流し，パイプの径や流速を変えながらその流れを観察することで，層流と乱流の間の遷移は

によって制御されることを見出した。 ここで$d$は管の径で，$u$は流れの平均速度，$\nu$は運動学的粘性である。 この無次元のパラメータ$Re$を，Reynolds数（Reynolds number）という。

ただし，乱流が最初に現れる$Re$の臨界値（臨界Reynolds数（critical Reynolds number））は，パイプの入り口における揺動にも強く依存する。 Reynoldsの実験では，典型的には$Re \sim 2000$程度になると乱流が発生するが，入口の揺動を最小にした場合，臨界値は$Re\sim13,000$まで上がることがわかった。 現在では，それを大きく上回る値（$\sim 10^5$）が実現されている。

Reynolds数(\ref{eq:reynolds_number})は，系を特徴づける長さ$L$と特徴的な流れの速さ$U$によって

と定義することで，Reynoldsが実験に用いたようなパイプに限らず，様々な幾何学的条件を持つ系に適用される。 この量を基にReynoldsが導いた相似則もまた，非常に重要な概念である。