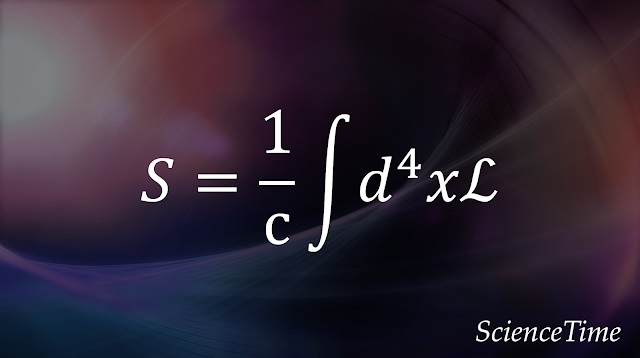Introduction
力学との類推により,場のLagrangianを導入し,そこから運動方程式と保存則と対称性に関する一般的な定理であるNoetherの定理を導く。
場のLagrangianと運動方程式
力学における粒子の運動方程式は,離散的な座標$x$とその1階の導関数である速度$\dot{x}$の関数Lagrangian $L$の積分,すなわち作用
\begin{align}
S=\int L(x,\dot{x}) dt
\end{align}
の変分を取ることで導かれた。
時空の各点に値を持つ連続的な場についても,それとの類推で,座標$x$に場$\phi(x)$を,速度$\dot{x}$に場の導関数$\pd_\mu \phi \ (\mu=0,1,2,3)$を対応させることで,場の作用を
\begin{align}
S= \int dt L(\phi, \pd \phi) = \frac{1}{c}\int d^4x \sL(\phi, \pd \phi)
\end{align}
と導入する。
ここで,$d^4x=dx^0 dx^1 dx^2 dx^3=cdt dx^1 dx^2 dx^3$である。
$\sL$は,体積積分を行うことで$L$になる量であるから,Lagrangian密度と呼ばれるが,場の理論では$L$よりも$\sL$を中心に扱うため,$\sL$の方を単にLagrangianと呼ぶことも多い。
力学の場合と同様に変分$\phi(x)\to \phi +\delta \phi(x)$を取ることで
\begin{align}
\delta S
=&
\frac{1}{c}\int d^4x
\left(\frac{\pd \sL}{\pd \phi}\delta \phi
+\frac{\pd \sL}{\pd (\pd_\mu \phi)} \delta\pd_\mu \phi\right) \notag \\
=&
\frac{1}{c}\int d^4x
\left(\frac{\pd \sL}{\pd \phi}
-\frac{\pd}{\pd x^\mu} \frac{\pd \sL}{\pd (\pd_\mu \phi)}\right)\delta \phi \notag \\
&+
\frac{1}{c}\int d^4x \frac{\pd}{\pd x^\mu}
\left(\frac{\pd \sL}{\pd (\pd_\mu \phi)} \delta \phi\right)
\end{align}
となり,最後の項は積分表面で$\delta \phi=0$とすることで落ちる。
変分$\delta \phi$の取り方は境界条件を除いて任意であることから,Euler-Lagrange方程式
\begin{align}
\pd_\mu \frac{\pd \sL}{\pd(\pd_\mu \phi)}
=
\frac{\pd \sL}{\pd \phi}
\end{align}
が得られる。
Noetherの定理
続いて,これも力学の場合と同様の議論により,場の理論に関するNoetherの定理を導く。
関数$G(\phi(x))$と無限小パラメータ$\ep$によって表される無限小変換
\begin{align}
\phi(x)\to \phi(x)+\ep G(\phi(x))
\end{align}
の下で,Lagrangianの変化,すなわち変換後のLagrangianと元のLagrangianとの差$\delta \sL$が
\begin{align}
\delta\sL=\ep \pd_\mu \sJ^\mu
\end{align}
のように,何らかの関数$\sJ^\mu$の4元発散の形に書けるならば,作用は不変にとどまる。
このときのLagrangianの変化分は,具体的に
\begin{align}
\delta \sL
=
\frac{\pd \sL}{\pd \phi}\ep G
+\frac{\pd \sL}{\pd (\pd_\mu \phi)} \ep\pd_\mu G
\end{align}
であり,右辺2項目を
\begin{align}
\frac{\pd \sL}{\pd (\pd_\mu \phi)} \ep\pd_\mu G
=
\ep \pd_\mu
\left( \frac{\pd \sL}{\pd (\pd_\mu \phi)} G\right)
-
\pd_\mu \left( \frac{\pd \sL}{\pd (\pd_\mu \phi)}\right) \ep G
\end{align}
を用いて並び替えると
\begin{align}
\delta \sL
=
\ep \pd_\mu
\left( \frac{\pd \sL}{\pd (\pd_\mu \phi)} G\right)
+
\ep \left[
\frac{\pd \sL}{\pd \phi}
-
\pd_\mu \left( \frac{\pd \sL}{\pd (\pd_\mu \phi)}\right)
\right] G
\end{align}
と表せる。
2項目はEuler-Lagrangian方程式より消えるため,関数$G$による変換で作用が不変なとき
\begin{align}
\pd_\mu j^\mu(x)=0
\end{align}
を満たす量,Noetherカレント
\begin{align}
\label {eq:N_current}
j^\mu
\equiv
\frac{\pd \sL}{\pd (\pd_\mu \phi)} G
-
\sJ^\mu
\end{align}
が存在することがわかる。
このときまた,Noetherチャージと呼ばれる保存量
\begin{align}
Q\equiv \int d^3x j^0
\end{align}
が定義できる。
実際,(\ref{eq:N_current})を用いて
\begin{align}
\frac{dQ}{dt}
=
c\pd_0 \int d^3x j^0
=
-\int d^3x \pd_i j^i
\end{align}
と時間微分を空間微分に置き換え,積分領域を境界におけるカレントが0となるほど十分大きくとれば,Gaussの定理を適用することで,$Q$が保存量であることが確認できる。