電磁波の方程式
ソース(電荷及び電流密度)のない場合の時間変動する電磁場の式
\begin{align}
\nabla \times \bm{E}
=& -\frac{\pd\bm{B}}{\pd t} \\
%
\nabla \times \bm{B}
=& \varepsilon_0 \mu_0
\frac{\pd\bm{E}}{\pd t}
\end{align}
について考える。
1つ目の式の回転を取ると,左辺は
\begin{equation}
\nabla\times(\nabla \times \bm{E})
= \nabla (\nabla\cdot\bm{E})
- \nabla^2 \bm{E}
\end{equation}
であり,右辺は
\begin{equation}
- \nabla \times \frac{\pd\bm{B}}{\pd t}
=
- \frac{\pd}{\pd t}(\nabla \times\bm{B})
=
-
\varepsilon_0 \mu_0
\frac{\pd^2}{\pd t^2}\bm{E}
\end{equation}
となる。
したがって
\begin{equation}
\label{eq:wave_eq_E}
\nabla^2 \bm{E}
-
\frac{1}{c^2}
\frac{\pd^2}{\pd t^2}\bm{E}
=0
\end{equation}
が成り立つ。
ここで$c=1/\sqrt{\varepsilon_0 \mu_0}$とした。
磁場の回転の式についても同様にして
\begin{equation}
\label{eq:wave_eq_B}
\nabla^2 \bm{B}
-
\frac{1}{c^2}
\frac{\pd^2}{\pd t^2}\bm{B}
=0
\end{equation}
を得る。
式(\ref{eq:wave_eq_E})および(\ref{eq:wave_eq_B})は,標準的な波動方程式であり,電磁場が波動として伝播することを示している。
$\varepsilon_0$と$\mu_0$の値はそれぞれ
\begin{equation}
\varepsilon_0
=8.8542\times10^{-12} \ \mathrm{C^2N^{-1}m^{-2}}
\end{equation}
\begin{equation}
\mu_0
=4\pi\times10^{-7} \ \mathrm{NA^{-2}}
\end{equation}
である。
よって,波の位相速度は
\begin{equation}
c
= \frac{1}{\sqrt{\varepsilon_0\mu_0}}
= 2.988 \times 10^{8} \ \mathrm{ms^{-1}}
\end{equation}
であり,光速に一致する。
リンク
Maxwellがこの結果を見出したとき,すでに$\varepsilon_0$と$\mu_0$の値は良く知られており,当時の観測精度で得られている光速の値とも非常に近いものであった。
また,スリットによる回折実験などから,可視光の波長範囲は,$400$-$760$nmという非常に狭いものであることもわかっていたが,Maxwellが見出した電磁場の波,すなわち電磁波の波長に制限はない。
これらのことからMaxwellは,光の実体は電磁波であり,我々は目に見える一部のスペクトル領域に属するものを,光として認識しているのだと主張した。
その仮説は,1888年,ドイツの物理学者Heinrich Rudolf Hertzの実験により実証された。
この驚くべき発見について Fitzpatrick (2010) はこう記述している:
彼は,それまで性質が不明であった光が,電磁放射の一形態であると推測した。
これは驚くべき予測だった。
何といってもMaxwellの方程式は,電荷,電池,コイル,電流など,光とは一見何の関係もなさそうに思われていたものを用いた,卓上の実験室実験の結果から導き出されたものなのである。
平面波解
電磁波の方程式(\ref{eq:wave_eq_E})および(\ref{eq:wave_eq_B})の,最も基本的な平面波解
\begin{equation}
\label{eq:EM_plane_wave}
\bm{E}
=\bm{E}_0 e^{i(\bm{k}\cdot\bm{x}-\omega t)},
\quad
\bm{B}
=\bm{B}_0 e^{i(\bm{k}\cdot\bm{x}-\omega t)}
\end{equation}
について考えてみる。
これらの発散を考えると,Gaussの法則$\nabla\cdot\bm{E}=0$および$\nabla\cdot\bm{B}=0$より
\begin{equation}
\bm{k}\cdot\bm{E}_0
=\bm{k}\cdot\bm{B}_0
=0
\end{equation}
が成り立つ。
これは,電磁場の変位は波の伝播方向に垂直であり,電磁波が横波であることを意味している。
また,回転を取った場合は
\begin{equation}
\nabla \times \bm{E}
+\frac{\pd\bm{B}}{\pd t}
=
i\left(
\bm{k}\times\bm{E}_0
-\omega\bm{B}_0
\right)e^{i(\bm{k}\cdot\bm{x}-\omega t)}
=0
\end{equation}
および
\begin{equation}
\nabla \times \bm{B}
-\frac{1}{c^2}\frac{\pd\bm{E}}{\pd t}
=
i\left(
\bm{k}\times\bm{B}_0
+\frac{\omega}{c^2}\bm{E}_0
\right)e^{i(\bm{k}\cdot\bm{x}-\omega t)}
=0
\end{equation}
より
\begin{equation}
\bm{B}_0=\frac{\bm{k}}{\omega}\times\bm{E}_0
\end{equation}
\begin{equation}
\bm{E}_0=-\frac{c^2}{\omega}\bm{k}\times\bm{B}_0
\end{equation}
となり,$\bm{E}_0$と$\bm{B}_0$は互いに直交することがわかる。
したがって,平面電磁波の伝播の様子は,次の図のように描写できる。
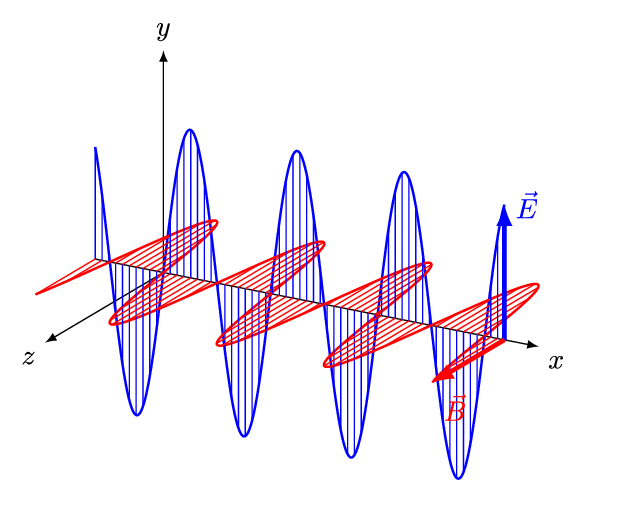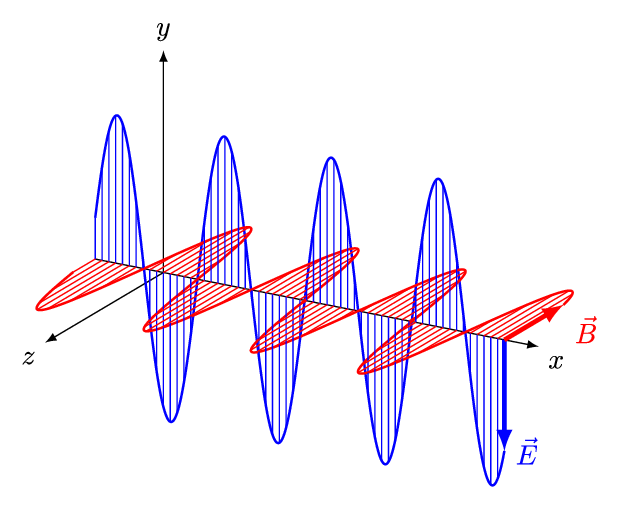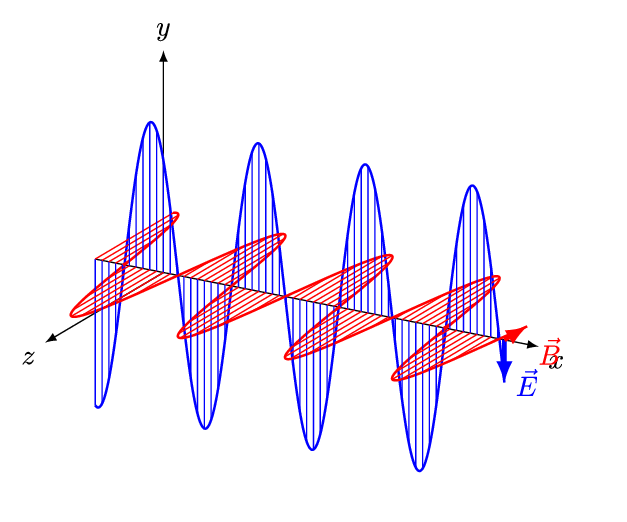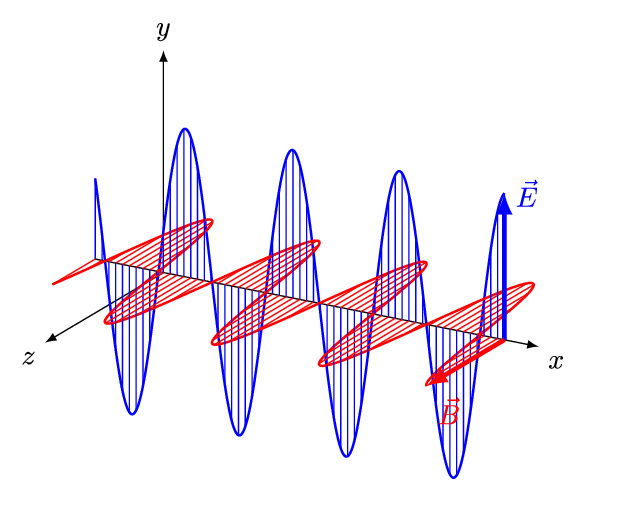
And1mu, CC BY-SA 4.0, via Wikimedia Commons
また,$\omega/k=c$より,電場と磁場の振幅の間に
\begin{equation}
\label{eq:E0_cB0}
E_0=cB_0
\end{equation}
の関係が成り立つこともわかる。
平面電磁波が運ぶエネルギーと運動量
電磁波が運ぶエネルギー密度
\begin{equation}
W
=\frac{B^2}{2\mu_0}
+\frac{\varepsilon_0 E^2}{2}
\end{equation}
を計算しよう。
場は振動しているから,1周期に渡る平均量
\begin{equation}
\overline{W}
=
\frac{1}{T}\int_0^T Wdt
\end{equation}
を求めることする。
ここで注意しなければならないのは,我々は便宜上,平面波を(\ref{eq:EM_plane_wave})のように複素関数で表しているが,物理的な波に対応するのはその実部であるということである。
したがって,エネルギー密度の式に含まれるような場の2乗の項を計算する際は,その実部同士を掛け合わせなくてはならない。
複素関数$A$の実部は
\begin{equation}
\label{eq:real_part_A}
\Re{(A)}=\frac{1}{2}(A+A^*)
\end{equation}
によって得られるから,ある複素ベクトル$\bm{A}=\bm{A}_0e^{-i\omega t}$と$\bm{B}=\bm{B}_0e^{-i\omega t}$の実部の積の周期平均は
\begin{equation}
\begin{split}
\overline{\Re{(\bm{A})}\cdot\Re{(\bm{B})} }
=&
\frac{1}{4}
\overline{(\bm{A}_0 e^{-i\omega t}+\bm{A}_0^* e^{i\omega t})
\cdot
(\bm{B}_0 e^{-i\omega t}+\bm{B}_0^* e^{i\omega t})} \\
%
=&
\frac{1}{4}(\bm{A}\cdot\bm{B}^*+\bm{A}^*\cdot\bm{B}) \\
%
=&
\frac{1}{2}\Re{(\bm{A}\cdot\bm{B}^*)}
\end{split}
\end{equation}
と計算できる。
2つ目の等式のところで,時間依存部分$e^{\pm i\omega t}$が残る項は周期平均によって消え,残らない部分は時間依存性を失うことから平均記号が外れている。
最後の等式では(\ref{eq:real_part_A})を再び用いている。
この関係を利用すると,場のエネルギー密度の周期平均は
\begin{equation}
\begin{split}
\overline{W}
=&
\overline{
\left(\frac{\varepsilon_0 E^2}{2}
+\frac{B^2}{2\mu_0}
\right)
} \\
%
=&
\frac{1}{4}
\Re{
(\varepsilon_0\bm{E}\cdot\bm{E}^*
+\frac{1}{\mu_0}\bm{B}\cdot\bm{B}^*)
} \\
%
=&
\frac{1}{2}
\varepsilon_0|E_0|^2
\end{split}
\end{equation}
と求められる。
ここで,電場と磁場の振幅の関係(\ref{eq:E0_cB0})を用いた。
続いてPoyntingベクトルについて考えよう。
複素ベクトルの実部の外積の時間平均についても,内積と同様の考えから
\begin{equation}
\overline{\Re{(\bm{A})}\times\Re{(\bm{B})}}
=
\frac{1}{2}\Re{(\bm{A}\times\bm{B}^*)}
\end{equation}
という関係が成り立つ。
したがって
\begin{equation}
\begin{split}
\overline{\bm{S}}
=&\frac{1}{2\mu_0}\Re{(\bm{E}\times\bm{B}^*)} \\
%
=&\frac{1}{2\mu_0 c}\Re{(\bm{E}\times(\hat{\bm{k}}\times\bm{E})^*)} \\
%
=&\frac{c\varepsilon_0}{2}|E_0|^2 \\
%
=& c \overline{W} \hat{\bm{k}} \\
\end{split}
\end{equation}
となる。
ここで,$\hat{\bm{k}}=\bm{k}/k$は波の進行方向の単位ベクトルである。
光速$c$で$\hat{\bm{k}}$方向に伝播する波にともなうエネルギー密度の流れとして非常にわかりやすい形をしている。

