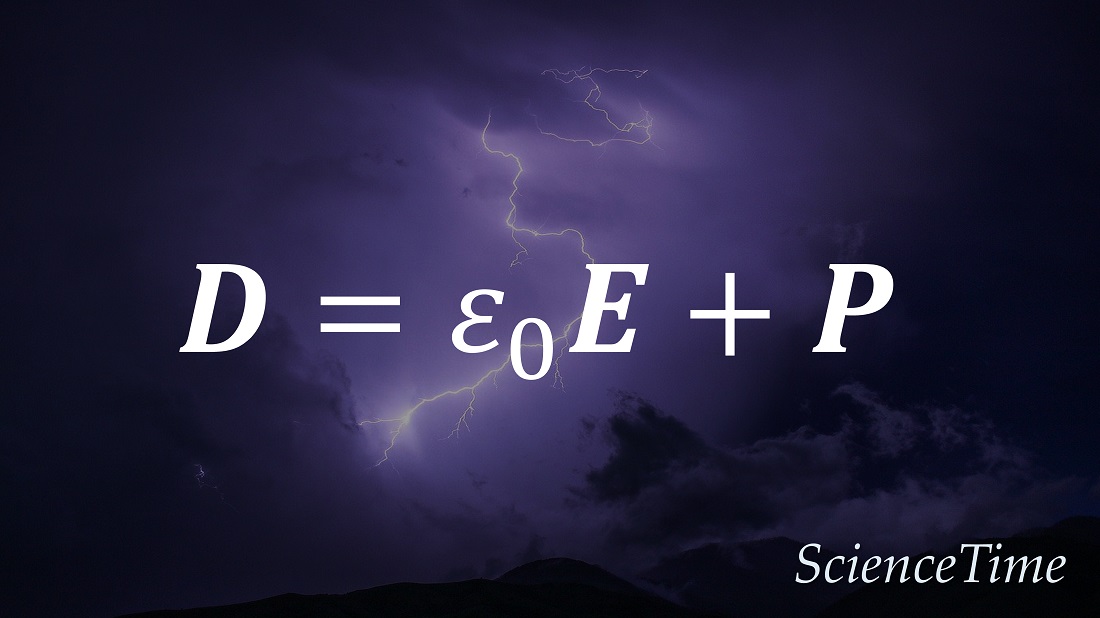束縛電荷
絶縁体内でも,マクロな静電場が満たす基本的な方程式は
\begin{equation}
\label{eq:nabla_E_delectric}
\nabla\times\bm{E}
=0
\end{equation}
および
\begin{equation}
\label{eq:macro_div_E}
\nabla\cdot\bm{E}
=\frac{\overline{\rho}}{\varepsilon_0}
\end{equation}
である。
ここでは,物質を構成する荷電粒子の存在のみを考え,外部から加えた自由な電荷がないものとする。
すると,絶縁体内の電荷は原子や分子内部に束縛されており,(\ref{eq:macro_div_E})の右辺に現れるのは束縛電荷だけとなる。
よって
\begin{equation}
\label{eq:macro_div_E_bound}
\nabla\cdot\bm{E}
=\frac{\overline{\rho}_\text{bound}}{\varepsilon_0}
\end{equation}
となる。
束縛電荷は原子領域内部ではある程度移動できるが,各原子・分子ごとには電気的に中性である。
したがって,物体の体積全体で積分すれば
\begin{equation}
\int\overline{\rho}_\text{bound}dV=0
\end{equation}
となる。
この条件は,物体に電場が作用していても成り立つ一般的なものである。
よって束縛電荷密度は,外部で0となるあるベクトル$\bm{P}$を用いて
\begin{equation}
\label{eq:div_P}
\overline{\rho}_\text{bound}
=-\nabla\cdot\bm{P}
\end{equation}
と書ける。
実際,物体を切断することなくすべて取り囲む閉曲面内部の体積$V$で積分すると
\begin{equation}
\label{eq:PndS}
\int_{V}\overline{\rho}_\text{bound}dV
=
-\int_{V} \nabla\cdot\bm{P}dV
=
-\oint_{\pd V} \ P_n dS
=
0
\end{equation}
となる。
このように$\bm{P}$は,物体外部ではゼロであり,物体全体で積分してもゼロであるという絶縁体の束縛電荷の性質を適切に反映している。
では,物体内部の任意の領域での性質はどうであろうか。
いたるところで$\bm{P}=0$であれば,表面を含めた任意の領域で電荷がゼロとなる。
これは物体に外的な電場が作用していない場合に対応する。
しかし,電場が作用すると状況は異なってくる。
分極と電気双極子
先に述べたように,束縛電荷も原子領域内ではある程度移動可能である。
よって電場をかけると,正電荷と負電荷がそれぞれ逆向きに力を受け,電荷の偏りを生む。
これを分極(polarization)とよぶ。
これは,絶縁体内部に多数の双極子モーメントが生まれることを意味する。
この性質のため,絶縁体は誘電体(dielectric)ともよばれる。
また,$\bm{P}$がゼロでないのは分極が生じている場合であり,それゆえ$\bm{P}$は分極ベクトル(polarization vector)と呼ばれる。
連続的に分布する双極子モーメントの和は$\int \overline{\rho}\bm{r}dV$で与えられる。
これに電荷密度と分極ベクトルの関係(\ref{eq:div_P})を代入し,再び積分範囲を物体全体を含む体積$V$とすると
\begin{equation}
\int_V \overline{\rho}_\text{bound}\bm{r}dV
=
-\int_V\bm{r}\nabla\cdot\bm{P}dV
\end{equation}
となる。
右辺の積分は成分($i,j=1,2,3$)で書くと
\begin{equation}
\begin{split}
-\int_V r_i \pd_j P_jdV
=&
-\int_V \pd_j(r_i P_j)dV
+\int_V P_j\pd_j r_idV \\
%
=&
-\int_{\pd V} r_i P_j dS_j
+\int_V P_j\delta_{ij} dV
\end{split}
\end{equation}
であり,右辺1項目は$\int_{\pd V}P_j dS_j=\int_{\pd V}P_ndS=0$より消える。
したがって
\begin{equation}
\int_V\overline{\rho}_\text{bound}\bm{r}dV
=
\int_V \bm{P}dV
\end{equation}
を得る。
すなわち,分極ベクトルは体積当たりの双極子モーメントを表していることが分かる。
分極が一様でなければ,すなわち$\bm{P}$が空間的に一様でなければ,(\ref{eq:div_P})より内部に電荷が生じる。
また,物体の表面を挟む2つの面をつないでできる微小体積で積分すると
\begin{equation}
\int\overline{\rho}_\text{bound}dV
=
\oint \sigma_\text{bound} dS
=
-\oint \bm{P}\cdot\bm{n} dS
\end{equation}
となり,外側では$\bm{P}\cdot\bm{n}=0$であるから,内側表面からだけの寄与$-\int\bm{P}\cdot(-\bm{n})dS$が残って
\begin{equation}
\sigma_\text{bound} = P_n
\end{equation}
となる。
分極電荷によるポテンシャル
点$\bm{r}'$近傍の微小体積$dV$中の双極子モーメントが,点$\bm{r}$作るポテンシャルは
\begin{equation}
d\phi(\bm{r},\bm{r}')
=
\frac{1}{4\pi\varepsilon_0}
\frac{\bm{P}(\bm{r})\cdot(\bm{r}-\bm{r}')}{|\bm{r}-\bm{r}'|^3}dV
\end{equation}
で与えられる。
これを空間全体で積分すれば,物体内のすべての双極子モーメントが作るポテンシャル
\begin{equation}
\phi(\bm{r})
=
\frac{1}{4\pi\varepsilon_0}
\int
\frac{\bm{P}(\bm{r})\cdot(\bm{r}-\bm{r}')}{|\bm{r}-\bm{r}'|^3}d^3r'
\end{equation}
が得られる。
ここで$\nabla'=\pd/\pd\bm{r}'$とし,$\nabla' |\bm{r}-\bm{r}'|^{-1}=(\bm{r}-\bm{r}')/ |\bm{r}-\bm{r}'|^3$の関係を使うと
\begin{equation}
\phi(\bm{r})
=
\frac{1}{4\pi\varepsilon_0}
\int
\bm{P}(\bm{r})\cdot\nabla'
\left(
\frac{1}{|\bm{r}-\bm{r}'|}
\right)d^3r'
\end{equation}
と変形できる。
さらに部分積分を実行すれば
\begin{equation}
\phi(\bm{r})
=
\frac{1}{4\pi\varepsilon_0}
\left[
-\int
\frac{\nabla'\cdot\bm{P}(\bm{r})}{|\bm{r}-\bm{r}'|}
d^3r'
+
\int
\frac{\bm{P}(\bm{r})\cdot\bm{n}}{|\bm{r}-\bm{r}'|}
dS
\right]
\end{equation}
を得る。
1項目は,分極が一様でない場合,内部の分極電荷からの寄与を与え,2項目が表面に現れる分極電荷の寄与を与える。
電気変位
(\ref{eq:div_P})を(\ref{eq:macro_div_E})に入れると
\begin{equation}
\label{eq:div_D_zero}
\nabla\cdot\bm{D}
=0
\end{equation}
ここで
\begin{equation}
\bm{D}
=\varepsilon_0\bm{E}+\bm{P}
\end{equation}
を定義した。
この$\bm{D}$は電気変位(electric displacement)や電束密度(electric flux density)あるいは電気誘導(electric induction)などと呼ばれる。
物質中に束縛されていない電荷や外部から加えられた自由な電荷$\overline{\rho}_\text{free}$がある場合
(\ref{eq:macro_div_E_bound})は
\begin{equation}
\nabla\cdot\bm{E}
=\frac{\overline{\rho}_\text{free}+\overline{\rho}_\text{bound}}{\varepsilon_0}
\end{equation}
となるから(\ref{eq:div_D_zero})も
\begin{equation}
\label{eq:div_D_rho_free}
\nabla\cdot\bm{D}
=\overline{\rho}_\text{free}
\end{equation}
に変更される。
境界条件
誘電体と別の物体あるいは真空との境界について考える。
境界を含む微小領域を考え,法線方向を$z$軸に取り,境界では$z=z_0$であるとする。
また,それぞれの領域の量に添え字1と2をつけて区別することにする。
まず,接触面に接な成分$E_t$であるが,電気変位の導入に伴っても,境界条件(\ref{eq:nabla_E_delectric})を変更する必要はない。
よって,導体における議論と同様にするか,あるいは積分形
\begin{equation}
\oint \bm{E}\cdot d\bm{l}=0
\end{equation}
を用いて,境界面をまたぎ,面に対して接方向と法線方向の経路からなる微小な長方形のループに沿って積分し,法線方向の長さ$h$を0に近づければ
\begin{equation}
h[E_{t1}(z=z_0+h/2)-E_{t2}(z=z_0-h/2)]
\to 0
\end{equation}
より,接成分が連続であるという条件
\begin{equation}
E_{t1}=E_{t2}
\end{equation}
を得る。
法線成分$D_n$については,(\ref{eq:div_D_rho_free})を底面$\Delta S$,高さ$h$の微小体積$\Delta V$で積分し,$\Delta S, h\to 0$とすると,左辺は
\begin{equation}
\begin{split}
\int_{\Delta V} dV \nabla\cdot\bm{D}
\simeq &
\Delta S \int_{-h/2}^{h/2}dz \frac{\pd D_n}{\pd z} \\
%
=&
\Delta S (D_{n1}-D_{n2})
\end{split}
\end{equation}
右辺は
\begin{equation}
\int_{\Delta V} dV \rho_\text{free}
\simeq
\Delta S \int_{-h/2}^{h/2}dz \rho_\text{free}
=
\Delta S \sigma_\text{free}
\end{equation}
よって
\begin{equation}
\label{eq:D1_D2_sigma_free}
D_{n1}-D_{n2}
=\sigma_\text{free}
\end{equation}
を得る。
ここで,$\sigma_\text{free}=\rho_\text{free}h$。
どちらも誘電体であれば自由電荷はないから(\ref{eq:D1_D2_sigma_free})は
\begin{equation}
D_{n1}=D_{n2}
\end{equation}
となる。