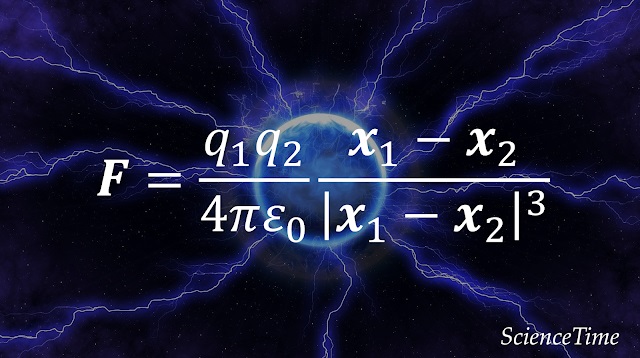静電気学の基礎：Coulomb力と静電場

Keywords:

リンク

Introduction

ここでは，静止した電荷に関する現象を記述する静電気学の基本概念を紹介する。はじめに静電気学の基本法則であるCoulomb力について解説したのち，電場やポテンシャルという概念についても簡単に説明する。

Coulomb力

電荷を持つ2つの物体同士には力が生じる。この力はそれらの物体が静止しているとき，以下の性質を持つことが経験的に確認できる。

力はそれぞれの物体の持つ電荷の大きさに比例する。
互いの電荷の符号が同じとき，力は反発しあう方向に，電荷の符号が反対の時，力は引き合う方向に働く。
力の大きさは，距離の2乗に反比例する。

電磁気学では，電荷の分布に広がりを無視するために，点電荷（point charge）と呼ばれる電荷だけあって大きさのない理想的な対象が扱われる。それぞれ電荷$q_1$と$q_2$を持ち，位置$\bm{x}_1$および$\bm{x}_2$に静止している2つの点電荷について考えると，上で挙げた性質を満たす力$\bm{F}$は

\begin{align} \label {eq:F1} \bm{F} = k \frac{q_1 q_2}{|\bm{x}_1-\bm{x}_2 |^2 } \frac{\bm{x}_1-\bm{x}_2}{|\bm{x}_1-\bm{x}_2 | } \end{align}

という式で表せる。これを，Coulombの法則といい，この力のことをCoulomb力，あるいは静電力（electrostatic force）という。 $k$は比例定数で

\begin{align} \frac{\bm{x}_1-\bm{x}_2}{|\bm{x}_1-\bm{x}_2 | } \end{align}

は，$\bm{x}_1$と$\bm{x}_2$を結ぶ単位ベクトルである。

比例定数も$k$経験的に求められるが，便宜的な理由から$4\pi$を抜きだし

\begin{align} \label {eq:k} k= \frac{1}{4\pi \varepsilon_0} \end{align}

という表し方をするのが標準的だ。 $4\pi$を抜きだして残る

\begin{align} \varepsilon_0 = 8.854\times 10^{-12} \ \ \text{F/m} \end{align}

を，真空中の誘電率（permittivity of vacuum）という

$\bm{r}=\bm{x}_1-\bm{x}_2$および$r=|\bm{r}|=|\bm{x}_1-\bm{x}_2|$とし，(\ref{eq:k})の形を採用すれば，(\ref{eq:F1})は

\begin{align} \bm{F} =& \frac{q_1 q_2}{4\pi \varepsilon_0}\frac{\bm{x}_1-\bm{x}_2}{|\bm{x}_1-\bm{x}_2 |^3 } \notag \\ \label {eq:F2} =& \frac{q_1 q_2}{4\pi \varepsilon_0 r^2 } \frac{\bm{r}}{r} \end{align}

とも書ける。

Coulomb力の大きさ

Coulomb力(\ref{eq:F2})は，万有引力

\begin{align} \bm{F}_G = G\frac{m_1 m_2}{r^2}\frac{\bm{r}}{r} \end{align}

と同様の形をしている。ここで$G=6.674\times 10^{-11}$m$^3$kg$^{-1}$s$^{-2}$は万有引力定数，$m_1,m_2$はそれぞれの物体の質量である。例えば$r=1$離れた電子（$e=−1.602\times 10^{-19}, m=9.109\times 10^{-31}$）と陽子（$e=1.602\times 10^{-19}, m=1.673\times 10^{-27}$）の間に働くCoulomb力と万有引力の大きさを考えると，Coulomb力は

\begin{align} F = \frac{(−1.602\times 10^{-19})^2}{4\pi\cdot 8.854\times 10^{-12}}\simeq 2.3 \times 10^{-28} \end{align}

であるのに対し

\begin{align} F_G = 6.674\times 10^{-11}\cdot 9.109\times 10^{-31}\cdot 1.673\times 10^{-27} \simeq 1.0 \times 10^{-67} \end{align}

となり，その比を取ると，Coulomb力の方が万有引力より$10^{39}$倍（$100$億かける$100$億かける$100$億かける$10$億倍！）以上も大きいことがわかる（比は距離によらない）。

複数の電荷から受ける力

複数の点電荷が存在するとき，ある点電荷が受ける力は，他の点電荷それぞれとの間に働く力の和で表せる。すなわち，位置$\bm{x}$にある電荷$q$を持つ点電荷の周りに$N$個の別の点電荷があるとき，周りの点電荷の位置と電荷をそれぞれ$\bm{x}_i$および$q_i, (i=1,2,...,N)$とすれば，$\bm{x}$にある電荷に働くCoulomb力は

\begin{align} \label {eq:Fi1} \bm{F}(\bm{x}) =\frac{q}{4\pi \varepsilon_0} \sum_{i=1}^N q_i \frac{\bm{x}-\bm{x}_i}{|\bm{x}-\bm{x}_i|^3} \end{align}

と表される。

電荷が連続的に分布している場合，点$\bm{x}'$を中心とする微小領域$d^3x'$にある電荷は，密度$\rho (\bm{x}')$を使って$\rho (\bm{x}') d^3x'$と表せる。これより，連続的な電荷分布の中にある点電荷が受けるCoulomb力は

\begin{align} \label {eq:Fi2} \bm{F}(\bm{x}) =\frac{q}{4\pi \varepsilon_0} \int \rho(\bm{x}') \frac{\bm{x}-\bm{x}'}{|\bm{x}-\bm{x}'|^3} d^3x' \end{align}

と表せる（図1参照）。

図1：$\bm{x}'$を中心とする体積$\Delta x_1 \Delta x_2 \Delta x_3$の微小立方体中の電荷をひとまとまりに$\Delta q$とし，(\ref{eq:Fi1})の要領で足し上げる操作を，$\Delta x_1 \Delta x_2 \Delta x_3 \to 0$として行うのが(\ref{eq:Fi2})

電場とスカラーポテンシャル

Coulomb力の表現(\ref{eq:Fi1})あるいは(\ref{eq:Fi2})は

\begin{equation} \bm{E}(\bm{x}) \equiv \sum_i \frac{q_i}{4\pi \varepsilon_0}\frac{\bm{x}-\bm{x}_i}{|\bm{x}-\bm{x}_i |^3 } \end{equation}

または

\begin{equation} \label{eq:E1} \bm{E}(\bm{x}) \equiv \frac{1}{4\pi \varepsilon_0} \int \rho(\bm{x}') \frac{\bm{x}-\bm{x}'}{|\bm{x}-\bm{x}'|^3} d^3x' \end{equation}

で定義される電場（electric field）という概念を導入すると

\begin{equation} \bm{F} = q \bm{E} \end{equation}

と書き換えることができる。

また，$\nabla =\pd/\pd \bm{x}$とすると

\begin{equation} \nabla \left( \frac{1}{|\bm{x}-\bm{x}'|}\right) = - \left( \frac{\bm{x}-\bm{x}'}{|\bm{x}-\bm{x}'|^3}\right) \end{equation}

であるから，電場(\ref{eq:E1})は

\begin{equation} \bm{E}(\bm{x}) = -\frac{1}{4\pi \varepsilon_0} \nabla \int \frac{\rho(\bm{x}') }{|\bm{x}-\bm{x}'|} d^3x' \end{equation}

と書き直せる。これより電場は，スカラー関数場$\phi(\bm{x})$を導入して

\begin{equation} \label{eq:E_nabla_phi} \bm{E} =-\nabla \phi \end{equation}

と表現することもできる。この$\phi$をスカラーポテンシャル（scalar potential）と呼ぶ。特に，電場が静的（時間に陽に依存しない）で，(\ref{eq:E_nabla_phi})のようポテンシャルの勾配のみで表されるようなとき，$\phi$は静電ポテンシャル（electrostatic potential）と呼ばれる。スカラーポテンシャルについてのより詳細な説明は『電磁ポテンシャルとゲージ変換』で行っている。

ポテンシャルエネルギー

重力の働く状況下では，物体を低いところから高いところまで移動するには仕事をしないといけない。あるいは，高いところにある物体は仕事をするためのエネルギーを持っているとも言える。重力ではなくCoulomb力が働く状況下でも同様のことがいえる%（仕事とエネルギーについてはコチラを参照）。 (\ref{eq:E_nabla_phi})より，Coulomb力$\bm{F}$が働く点粒子を点$A$から$B$まで運ぶのに要する仕事は，スカラーポテンシャルを用いて

\begin{equation} \begin{split} W =& -\int_A^B \bm{F}\cdot d\bm{x} \\ =& -q\int_A^B \bm{E}\cdot d\bm{x} \\ =& -q (\phi(B) -\phi(A) ) \end{split} \end{equation}

と求められる。

よって，点$A$を$\phi=0$となる無限遠に取ってしまえば，点$\bm{x}_i$にある点電荷の持つポテンシャルエネルギーは

\begin{equation} q_i \phi(\bm{x}_i) =-q_i\int_{-\infty}^{\bm{x}_i} \bm{E}(\bm{x})\cdot d\bm{x} = \frac{q_i}{4\pi \varepsilon_0}\sum_{i\neq j} \frac{q_j}{|\bm{x}_i - \bm{x}_j|} \end{equation}

となる。複数の点電荷から成る系の全ポテンシャルエネルギー$V$を求めるには，各電荷間に生じるポテンシャルエネルギーの和を取ってやればいい。ここで，和の取り方として

\begin{equation} V= \frac{1}{4\pi \varepsilon_0}\sum_{i,j} \frac{q_i q_j}{|\bm{x}_i - \bm{x}_j|} \end{equation}

とすると，$i=j$となって分母が発散してしまうケースが排除されていないことに加え，同じ組み合わせが2回ずつカウントされてしまうことに注意しよう（図2参照）。そのため，和の表現を

\begin{equation} V= \frac{1}{4\pi \varepsilon_0}\sum_{i}\sum_{(i < ) j} \frac{q_i q_j}{|\bm{x}_i - \bm{x}_j|} \end{equation}

と書き換えるか，以下のように2重にカウントした分を相殺するために2で割る必要がある。

\begin{equation} V= \frac{1}{8\pi \varepsilon_0}\sum_{i \neq j}\frac{q_i q_j}{|\bm{x}_i - \bm{x}_j|} \end{equation}

これに対応する連続的な表現は

\begin{equation} V= \frac{1}{8\pi \varepsilon_0} \int \frac{ \rho(\bm{x}) \rho(\bm{x}')}{|\bm{x}-\bm{x}'|} d^3x d^3x' \end{equation}

である。

図2：$N=3$のときの，$(i,j)$の組み合わせ

References

Jackson, J. D. (1999). Classical Electrodynamics. 3rd ed. John Wiley & Sons
――(2002, 2003). 電磁気学上/下. ‎ 西田稔訳. 吉岡書店.

Landau, L. D., & Lifshits, E. M. (1975). The Classical Theory of Fields (Course of Theoretical Physics). 4th ed. (6th Russian ed.) Oxford: Pergamon press.
――(1978). 場の古典論 (ランダウ=リフシッツ理論物理学教程) . ‎ 恒藤敏彦ほか訳. 東京図書.