Introduction
一般に,大気の鉛直方向の運動の時間スケールは,水平方向の運動の時間スケールに比べて非常に小さい。 そのため,鉛直方向には力学的なつり合いが成り立っていると仮定できる。静力学方程式と静水圧平衡
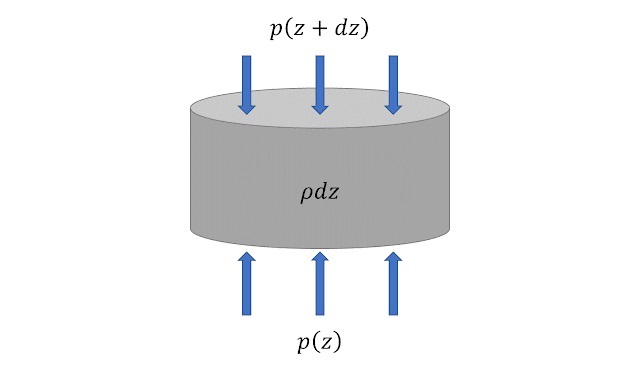
高さ$z$から$z+dz$のところに単位面積を低面積とする円柱を取ると,そこに含まれる大気分子の総質量は,質量密度$\rho$を用いて$\rho dz$と書ける。 高さ$z$において,下からこの円柱にかかる力は圧力$p(z)$に等しいが,この圧力は,$z+dz$で上から円柱にかかる圧力と,円柱に含まれる大気分子の重さを合わせたものを支えないといけない。 すなわち,高さ$z$で大気が力学的に釣り合うためには
\begin{equation}
\label{eq:pz_balance}
p(z)
=p(z+dz)
+\rho gdz
\end{equation}
が成り立つ必要がある。 ここで$g$は重力加速度である。 (\ref{eq:pz_balance})の右辺一項目を
\begin{equation}
p(z+dz)\simeq
p(z)
+\frac{dp}{dz}dz
\end{equation}
と展開し,並び替えることで
\begin{equation}
\label{eq:dpdz_rhog}
\frac{dp}{dz}
=
-\rho g
\end{equation}
が得られる。 これを,静力学方程式(hydrostatic equation)といい,これが成り立つ状態を静水圧平衡(hydrostatic balance)という。
状態方程式$\rho=p/(RT)$を用いて(\ref{eq:dpdz_rhog})から質量密度を消去すると
\begin{equation}
\frac{dp}{dz}
=
-\frac{pg}{RT}
\end{equation}
となり,これを積分することで
\begin{equation}
p(z)
=
p_s\exp
\left(-\int_{z_s}^z \frac{dz'}{H(z')} \right)
\end{equation}
を得る。 ここで,$z_s$は地表高度,$p_s=p(z=z_s)$そして
\begin{equation}
H(z)
=\frac{RT(z)}{g}
\end{equation}
はスケールハイト(scale height)と呼ばれる。