フィードバックと放射強制力

はじめに

ここでは，放射強制力，フィードバックパラメータおよび気候感度という気候変動の要因とそのインパクトの大きさを見積もる上で特に重要となる概念について説明する。

keywords: 気候変動, 地球, 大気物理学, 放射強制力, 気候感度, 気候フィードバック

内容

フィードバックパラメータ

大気上端における正味の下向きのフラックスを

\begin{align} Q\equiv F^\downarrow-F^\uparrow \end{align}

とする。 $Q$は，温度$T$に加え，温度$T$に加え，太陽定数や温室効果ガス濃度など，気候を左右する様々なパラメータに依存する。ここでは，簡単のために何らかのパラメータを1つ取り，それを$G$と表すことにしよう：$Q=Q(T,G)$。

はじめ温度$T_0$で平衡状態にあった系において，$G$の摂動$\delta G$が加わったことにより，温度が$T_0+\delta T$と変化したとする。このとき

\begin{align} Q(T_0+\delta T,G+\delta G) =Q(T_0,G)+\frac{\pd Q}{\pd T}\delta T +\frac{\pd Q}{\pd G}\delta G \end{align}

とし，エネルギーバランスの式

\begin{align} C\frac{dT}{dt}=F^\downarrow-F^\uparrow \end{align}

に代入することで，$\delta T$についての式

\begin{align} \label {eq:delT} C\frac{\pd \delta T}{\pd t} =\frac{\pd Q}{\pd T}\delta T +\frac{\pd Q}{\pd G}\delta G \end{align}

を得る。このとき，フィードバックパラメータを

\begin{align} \label {eq:lambda} \lambda \equiv -\frac{\pd Q}{\pd T} \end{align}

で定義する。温度変化に伴う正味のフラックスの変化が正であれば$\lambda < 0$，負であれば$\lambda > 0$である。

これを用いると(\ref{eq:delT})は

\begin{align} C\frac{\pd \delta T}{\pd t} =-\lambda \delta T +\frac{\pd Q}{\pd G}\delta G \end{align}

と表せる。左辺と右辺1項目の関係を見ると，正の$\lambda$は，温度変化を抑制する方向に，負の$\lambda$は温度変化を益々増大させる方向に作用することがわかる。

初期の$Q$の変化が温度を変化させ，その温度変化に伴ってさらに$Q$が変化を起こす，という変化のループが温度変化を益々促進することを，正のフィードバック（positive feedback），温度変化を減衰させることを負のフィードバック（negative feedback）という。実際のプロセスにおいては$G$に対応する複数のパラメータが関与し，これらのフィードバックが釣り合い，新たにエネルギーの釣り合いが得られたとき，系は新たな平衡温度に落ち着く。

気候感度と放射強制力

$G$の変化に伴う放射強制力（radiative forcing）を

\begin{align} \label {eq:radF} \delta F \equiv \frac{\pd Q}{\pd G}\delta G \end{align}

で定義すると，(\ref{eq:delT})は

\begin{align} C\frac{\pd \delta T}{\pd t} =\delta F-\lambda \delta T \end{align}

となり，系が新たな平衡状態に落ち着いたなら

\begin{align} \delta F=\lambda \delta T \end{align}

が成り立つ。

フィードバックパラメータの逆数

\begin{align} \label {eq:sensitivity} \lambda^{-1} = -\left( \frac{\pd Q}{\pd T} \right)^{-1} \end{align}

は気候感度（climate sensitivity）と呼ばれる。これを用いると，放射強制力に対する温度変化の関係

\begin{align} \delta T= \lambda^{-1} \delta F \end{align}

が得られる。

放射強制力の推定値

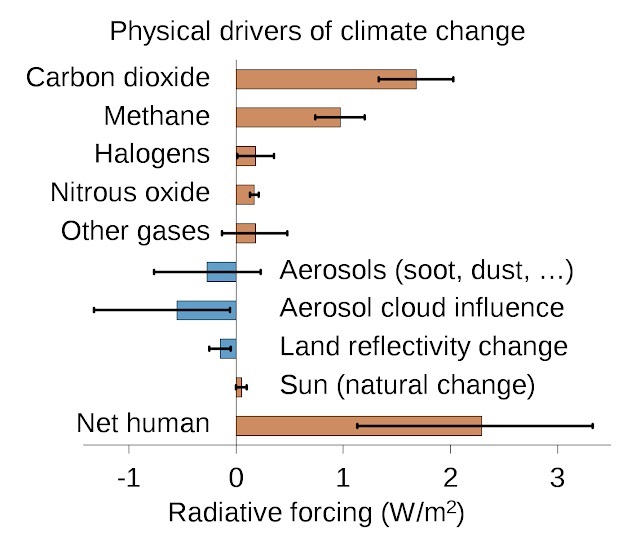
トップ画あるは下の図1は，IPCC第5次評価報告書でまとめられた，放射強制力の見積もりを表している。値は，産業革命以前（1750年）を基準とした2011年時点での全球平均となっている。値が正のものは温暖化に，負のものは寒冷化に寄与する。

太陽放射の影響を比較しても，二酸化炭素や畜産を主な排出源とするメタンといった温室効果ガスの影響を中心とする人為的影響の大きさは圧倒的である。しかも，人為的な影響の総合値は，前回（IPCC 2007）の報告時よりもさらに増加している。

最近まで，CO$_2$を倍増したときの強制力$\Delta F_{2\times \text{CO}_2}$に対応する温度変化$\Delta T$の推定値は，$1.5$℃から$4.5$℃と幅のあるものだった。しかし，先日発表された，数年に渡る詳細な研究の結果，気候感度の推定がより厳密なものとなり，$\Delta T$の推定値の値は$2.6$℃から$4.1$℃の幅まで狭められた（Sherwood et al. 2020）。この研究では，最良の推定は$3$℃よりわずかに上の温度で，$2$℃を下回る見込みは5%以下，$4.5$℃を上回る見込みは6-18%となること示されている。つまり，これまでの最も楽観的なシナリオはほぼ排除され，壊滅的なシナリオがより確実なものであると示されたことになる。

CO$_2$濃度は産業革命以前と比較し，2060年頃には倍の値に達する。ホモ・サピエンスは他の動物たちを道連れにしながら，相変わらず意気揚々と破滅的に向かう道を歩んでいる。

図1：1750年を基準とした2011年時点での放射強制力。『IPCC第5次評価報告書　第1作業部会報告書　政策決定者向け要約　気象庁訳』より転載

フィードバックと放射強制力

フィードバックパラメータ

気候感度と放射強制力

放射強制力の推定値

参考文献