1. ノート一覧
  2. 数学
  3. 位相幾何学

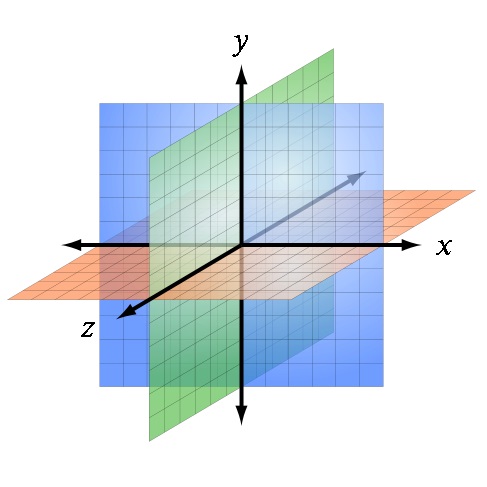
Euclid空間

Dr. SSS 2020/11/21 - 11:45:14 7114 位相幾何学
I, Sakurambo, CC BY-SA 3.0 , via Wikimedia Commons
はじめに

実数の集合$R$を考え，$R$の中の適当ないくつかの元$a,b,c,...$を取り出すと，その値を比べることで$a$と$b$の方が，$b$と$c$より互いに近い数などと判断できるように思える。 しかし，集合とは文字通りものの集まりでしかなく，集合それ自体には「近さ」や「長さ」を定量的に与えるものは何も備わっていない。 そこで，それらの量を扱うために，（非常に直感的な形で）「距離」や関連する概念を導入したものが，単なる数の集まりではないEuclid空間と呼ばれるものである。

これが実数のペアの集合$R^2$であれば，適当なペアを$(x_1,y_1),(x_2,y_2),(x_3,y_3)...$と取ってそれらを平面上の点とみなし，点から点を線でつなぐことで，「方向」や線と線がなす「角度」といった概念を考えることもできるようになる。 より高次の集合$R^n$についても同様だ。

このように，実数の集まり$R^n$に，特定の幾何学的構造を導入したものがEuclid空間であるということである。 Euclid空間を指すとき，単なる集合としての$R^n$と区別するため，$E^n$という記号が用いられることもある（下図参照。ただし，以下では$E^n$という記法用いない）。

以下，距離や長さなどの定義を，より形式的な形で説明する。

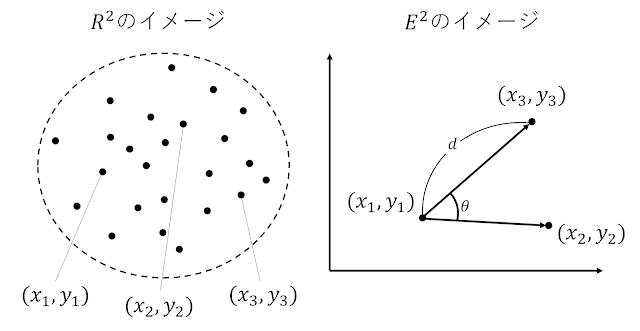
図1：実数のペアの集合のイメージ（左）と，2次元Euclid空間のイメージ（右）


keywords: 位相空間, 内積, ベクトル空間, 幾何学, 距離空間, Euclid空間

内容

数空間と点

実数全体の集合を$R$で表す。 $R$の各元を直線上の各点と1対1に対応付けることで，対応する$R$の元と直線上の点を同一視することが出来る。 $R^2=R\times R$の元も同様に，2つの直交する直線を軸とする平面上の点と，$R^2$に含まれる2つの実数の組$(x_1,x_2)$と対応付けができる。 これを一般化し，$n\geq 1$の自然数について$R^n$を$n$次元数空間といい，これの元$(x_1,...,x_n)$を$R^n$の点という。 点をまとめて

\begin{align} \bm{x}=(x_1,...,x_n) \end{align}

のようにも表し，$x_i$を$\bm{x}$の$i$成分という。 また，すべての成分が0である点$(0,...,0)$を原点（origin）といい，$O$で表す。


距離

$R^n$の$2$点$\bm{x}=(x_1,...,x_n)$と$\bm{y}=(y_1,...,y_n)$の間の距離（distance）または計量（metric）$d(\bm{x},\bm{y})$を

\begin{align} \label{eq:Euclid_d} d(\bm{x},\bm{y}) =\sqrt{(x_1-y_1)^2+(x_2-y_2)^2+...+(x_n-y_n)^2} \end{align}

で定義する。 距離は以下の基本的な性質を満たす：

  • $d(\bm{x},\bm{y})\geq 0$で，$d(\bm{x},\bm{y})=0$となるのは$\bm{x}=\bm{y}$の場合に限る。
  • $d(\bm{x},\bm{y})+d(\bm{y},\bm{z}) \geq d(\bm{x},\bm{z})$
  • $d(\bm{x},\bm{y})=d(\bm{y},\bm{x})$

上の性質を満たす距離が定義される集合をを距離空間（metric space）というが，上の性質を満たす距離の定義はいくつもあるため，(\ref{eq:Euclid_d})で定義される距離は，それらと区別してEuclid距離（Euclidean distance）やEuclid計量（Euclidean metric）と呼ばれる。


ベクトルと内積

$R^n$の任意の2元$\bm{x}=(x_1,...,x_n)$，$\bm{y}=(y_1,...,y_n)$と$a\in R$に対して，スカラー倍と和をそれぞれ

\begin{align} a\bm{x}=(ax_1,...,ax_n) \end{align}

\begin{align} \bm{x}+\bm{y}=(x_1+y_1,...,x_n+y_n) \end{align}

と定義すれば，$R^n$はベクトル空間の定義を満たす。 このようなベクトル空間としてみるとき，$R^n$を$n$次元数ベクトル空間といい，その元を$n$次元数ベクトルという。

ベクトル$\bm{x} \in R^n$に対し

\begin{align} \| \bm{x} \| = (x_1^2+...+x_n^2)^{1/2} \end{align}

を，$\bm{x}$のノルムあるいは長さという。 ノルムは以下の3つの基本的な性質を満たす

  • $\| \bm{x} \| \geq 0$で， $\| \bm{x} \| = 0$となるのは$\bm{x}=0$のときかつそのときに限る。
  • $\| a\bm{x}\|=a\| \bm{x} \|$
  • $\| \bm{x} +\bm{y} \| \leq \| \bm{x} \|+\| \bm{y} \|$$

また，$R^n$の任意の2元$\bm{x}=(x_1,...,x_n)$と$\bm{y}=(y_1,...,y_n)$に対して

\begin{align} \langle \bm{x}, \bm{y} \rangle = x_1y_1+...+x_n y_n \end{align}

を，$\bm{x}$と$\bm{y}$の内積（inner product）という。 この内積は，対称性

\begin{align} \langle \bm{x}, \bm{y} \rangle = \langle \bm{y}, \bm{x} \rangle \end{align}

および双線形性

\begin{align} \langle a\bm{x}+b\bm{y}, \bm{z} \rangle = a\langle \bm{x}, \bm{z} \rangle + b\langle \bm{y}, \bm{z} \rangle \end{align}

を満たす。

このとき

\begin{align} \cos\theta=\frac{\langle x,y\rangle}{\| \bm{x} \|\| \bm{y} \|} \end{align}

で与えられる$\theta$を，$\bm{x}$と$\bm{y}$のなす角（angle）という。

このように内積が定義されているベクトル空間を内積空間という。 そして，内積空間としての$R^n$を，単なる実数の組の集合と区別して，$n$次元Euclid空間という。

参考文献

  1. ノート一覧
  2. 数学
  3. 位相幾何学