内部、境界、閉包

内部，境界，閉包の定義

トップ画は，以下で紹介する概念のいくつかに関するイメージになっているため，その都度参照しながら読み進めてもらいたい。

内点と内部

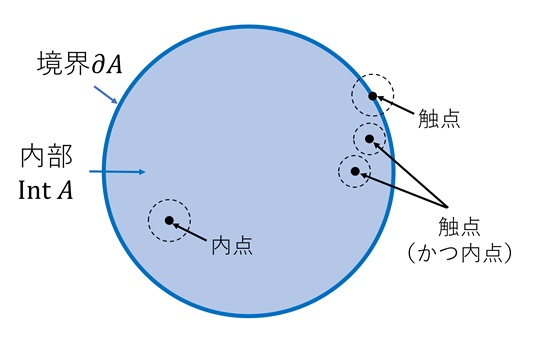
$X$を距離空間，$A$をその部分集合とする。 $X$の点$x$が$U \subset A$となる近傍$U$を持つとき，$x$を$A$の内点（interior point）という。 そして，$A$の内点全体の集合を$A$の内部（interior）と呼び，$\text{Int} A$と表す。

触点と閉包

また，任意の近傍$U$に対して

となる点，すなわちどんなに小さな近傍を取っても，$A$の点を含んでしまうような点$x$を，$A$の触点（adherent point）という。 そして，$A$の触点全体を，$A$の閉包（closure）といい，$\bar{A}$で表す。

触点と良く似た概念として集積点というものがあったが，$A \subset X$の集積点とは，$x$の任意の近傍$U$が$x$以外の$A$の点を含むもの，すなわち

となる$x\in X$と定義されていたため，異なる概念である。 実際，(\ref{eq:def_accum_point})が成り立てば(\ref{eq:def_adh_point})も成り立つため，集積点であれば触点でもあるが，部分集合として1点$x\in X$だけからなるような集合$A=\{x\}$を考えると，(\ref{eq:def_adh_point})は成り立つが(\ref{eq:def_accum_point})は成り立たないため，触点であるからといって集積点でもあるとは言えない。 この例のように，$A$の点であるが$A$の集積点とはならない点を，$A$の孤立点（isolated point）という。

定義の通り，その近傍が$A$と共通部分を持っていればいいので，触点自体が内部に含まれている必要はなく，$\bar{A}$から$A$の内部を取り除いた $$ \pd A\equiv \bar{A}-\text{Int} A $$ を$A$の境界（boundary）と呼ぶ。

包含関係

定義からわかるように，$A$とその内部および閉包との間には

という包含関係が成り立つ。

開集合と閉集合の定義

近傍と開集合

境界という概念を用いて，開集合と閉集合が次のように定義される：

(\ref{eq:A_rel})の関係で見ると，$\text{Int}A = A$が成り立つものが開集合，$A= \bar{A}$が成り立つのが閉集合である。