距離空間の間の連続写像

Keywords:

Introduction

ここでは，距離空間の間の連続写像について説明する。はじめに，最も直感的と思われる表現を与え，それに続いて，いくつかの同値だが異なる表現と，それらの間の関係を解説する。

まず，最も直感的と思われる定義を与えよう。

定義：距離空間$X$から別の距離空間$Y$への写像$f:X\to Y$を考える。写像$f$が，$X$の任意の点列$\{x_n\}$に対して

\begin{align} \lim_{n\to \infty}x_n\to x \quad \text{ならば} \quad \notag \\ \label{eq:limit_x} \lim_{n\to \infty}f(x_n)\to f(x) \end{align}

を満たすとき，$f$を連続写像（continuous map）という。

(\ref{eq:limit_x})における$x$のような点列の極限というのは，近傍という概念を用いて定義されるのであった。よって，写像の連続性についても，同様の観点から記述できることが期待される。

実際，(\ref{eq:limit_x})は次のことと同値である：

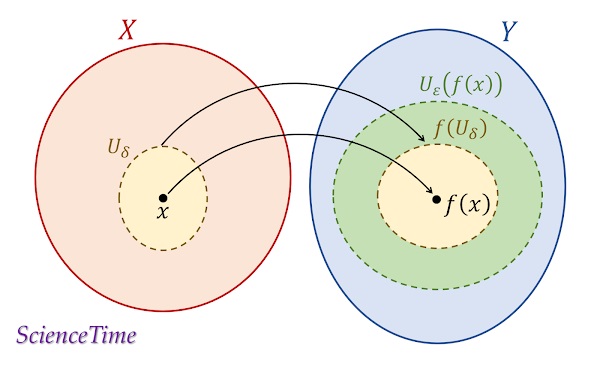
$f(x)$の任意の$\varepsilon$-近傍$U_\varepsilon(f(x))$，に対し，適当な正数$\delta$を取ると

\begin{align} \label{eq:map_neigboor} f(U_\delta (x)) \subset U_\varepsilon(f(x)) \end{align}

が成り立つ。

これは，$X$の任意の点$x$に対して，その近傍$U_\delta (x)$を取ると，$U_\delta (x)$に含まれる任意の別の点$x'$の像$f(x')$が，$f(x)$の近傍$U_\varepsilon(f(x))$の内部に含まれるということを言っている（トップ画参照）。

proof (\ref{eq:limit_x})ならば(\ref{eq:map_neigboor})を証明するために，(\ref{eq:map_neigboor})が成り立たない場合，すなわち

\begin{align} \label{eq:anti} f(U_\delta (x)) \not\subset U_\varepsilon(f(x)) \end{align}

を仮定して考えてみる。

自然数$n$に対して$\delta=1/n$と取ると，(\ref{eq:anti})が成り立つということは，ある$n$において
\begin{align} x_n \in U_{1/n}\quad \text{かつ} \quad f(x_n) \not\subset U_\varepsilon(f(x_n)) \end{align}
となる点$x_n$が存在するということである。
つまり
\begin{align} d(x,x_n) < 1/n \quad \text{かつ} \quad d(f(x),f(x_n))\geq \varepsilon \end{align}
となる$\varepsilon>0$が存在するということである
しかし，これは，$n\to \infty$の極限を取ったとき，$d(x_n,x)\to 0$ならば，$d(f(x_n),f(x))\to 0$であるという連続写像の定義(\ref{eq:limit_x})に反する。
よって，(\ref{eq:limit_x})ならば(\ref{eq:map_neigboor})と言える。

次に，(\ref{eq:map_neigboor})ならば(\ref{eq:limit_x})を示そう。

$\lim_{n\to \infty} x_n \to x$となる$X$の任意の点列を取ると，(\ref{eq:map_neigboor})は任意の正数$\varepsilon$に対し
\begin{align} d(x,x_n) < \delta \quad \text{ならば} \quad d(f(x),f(x_n)) < \varepsilon \end{align}
となる正数$\delta$が決まるということを示している。
$\lim_{n\to \infty} x_n \to x$とは，ある数$k$に対して
\begin{align} k < n \quad \text{ならば} \quad x_n \in U_\delta(x) \end{align}
となるということであるから
\begin{align} k < n \quad \text{ならば} \quad f(x_n) \in U_\varepsilon(f(x)) \end{align}
が成り立つ。
$\varepsilon$の取り方は任意であったから，これは$\lim_{n\to \infty} f(x_n) \to f(x)$が成り立つことを示している。
よって，(\ref{eq:map_neigboor})ならば(\ref{eq:limit_x})である。

□

上の議論は，$X=Y=R$であるとき，$x=a$で$f$が連続なら，任意の正数$\varepsilon$に対して，ある正数$\delta$が存在し

\begin{align} |x-a|<\delta \quad \text{ならば} \quad |f(x)-f(a)| <\varepsilon \end{align}

が成り立つ，といういわゆる$\varepsilon$-$\delta$論法に対応している。

距離空間$X$から別の距離空間$Y$への写像$f$が連続であるということは，次のこととも同値である：

proof (\ref{eq:limit_x})ならば(i)を示す。

$Y$の任意の開集合$V$に対し，$x \in f^{-1}(V)$とする。 $f(x)\in V$で，$V$は開集合であるから， $$ U_\varepsilon(f(x)) \subset V $$ となる近傍$U_\varepsilon(f(x))$が存在する。
このとき，連続性の定義より，ある正数$\delta$が存在し， $$ f(U_\delta(x))\subset U_\varepsilon(f(x)) $$ が成り立つ。
したがって $$ f(U_\delta(x))\subset V $$ となる。
これは
\begin{align} U_\delta(x)\subset f^{-1}(V) \end{align}
と表すこともできるが，$x$は$f^{-1}(V)$内の任意の点であったから，$f^{-1}(V)$は開集合であるとわかる。
よって，(\ref{eq:limit_x})ならば(i)である。

続いて，(i)ならば(\ref{eq:limit_x})を示す。

任意の$x\in X$に対し，$V$を$f(x)$の近傍$V=U_\varepsilon(f(x))$とする。
仮定より，$f^{-1}(V)$は開集合であるから，適当な正数$\delta$を取ると $$ U_\delta(x) \subset f^{-1}(V) $$ となる。
よって，$f(U_\delta(x)) \subset V$，すなわち $$ f(U_\delta(x)) \subset U_\varepsilon(f(x)) $$ が成り立つ。

最後に，(i)と(ii)が同値であることを示す。

閉集合$W\subset Y$の補集合$Y-W$は$Y$の開集合であるから，(i)より$X-f^{-1}(W)=f^{-1}(Y-W)$は$X$の開集合である。
よって，$f^{-1}(W)$は閉集合である。
反対に，開集合$V\subset Y$の補集合$Y-V$は$Y$の閉集合であるから，(ii) より$X-f^{-1}(V)=f^{-1}(Y-V)$は$X$の閉集合である。
よって，$f^{-1}(V)$は開集合である。
これより，(i)であれば(ii)も，(ii)であれば(i)も成り立つ。

□

Adams, C. and Franzosa, R. (2007). Introduction to Topology: Pure and Applied. Prentice Hall.

松本幸夫. (1988). 多様体の基礎. 東京大学出版会.

Schutz, B. F. (1980). Geometrical Methods of Mathematical Physics.‎ Cambridge University Press.
――(1987). 物理学における幾何学的方法. 家正則, 観山正見, 二間瀬敏史訳. 吉岡書店.

志賀浩二. (1988). 位相への30講. 朝倉書店.

Sutherland, W. A. (2009). Introduction to Metric and Topological Spaces. Oxford University Press.

内田伏一. (2020). 集合と位相(増補新装版). 裳華房.