Introduction
ここでは,コンパクト空間について説明する。 まずコンパクト空間の定義を示したのち,Euclid空間を用いた例といくつかの定理を紹介し,最後にEuclid空間の部分集合がコンパクトであることと,有界閉集合であることが同値であることを示す。
コンパクト性
定義:位相空間$X$が部分集合の族$\ \sU=\{U_i \ | \ i\in I\}$によって覆ってしまえるとき,つまり
が成り立つとき,$\sU$を$X$の被覆(cover)という。 特に,各$U_i$が開集合のとき,$\sU$を開被覆(open cover)という。
有限個からなる開被覆を有限開被覆(finite open cover)という。 また,ある開被覆$\{U_i \ | \ i\in I\}$に有限開被覆$\{U_j \ | \ j\in J \}$を構成できる有限の部分集合$J\subset I$があるとき,$\{U_j \ | \ j\in J\}$を有限部分被覆(finite subcover)という。
これらの概念を用いて,次の定義が与えられる:
定義:位相空間$X$の任意の開被覆$\{U_i \ | \ i\in I\}$が有限部分被覆を持つとき,$X$はコンパクト(compact)であるという。 また,コンパクトな位相空間をコンパクト空間(compact space)という。
定義:$X$を位相空間,$A$をその部分集合とする。 $X$の位相の部分集合$\sU=\{U_i \ | \ i\in I\}$が$A$の開被覆となり,任意の開被覆が有限部分被覆を持つとき,$A$はコンパクトであり,$X$のコンパクト部分集合(compact subset)であるという。
これらの定義は,ある集合の開被覆が単に有限開被覆を持つといっているのではなく,「任意の」開被覆から有限部分被覆を取れるといっていることに注意してほしい。
例えば次の例は,有限の開集合(例えば自分自身)で被覆することはできるが,コンパクトではない。
例:通常の位相に関して,開区間$(a,b)\subset R$はコンパクトではない。 つまり,有限部分被覆を持たない開被覆を持つ。
proof
- $U_n=(a,b-1/n), n\in N$という開集合から集合族を考えると,これは開区間$(a,b)$の開被覆となる。
- 実際,任意の$x \in (a,b)$に対して,十分大きな$n$を取れば$x \in (a,b-1/n)$となる。
- しかし,有限個の$U_n$だけでは,決して全体を被覆することはできないため,開区間はコンパクトではない。
対して,次の定理が成り立つ:
定理1:通常の位相に関して,開区間$[a,b]\subset R$は$R$のコンパクト部分集合である。
proof
- 矛盾を導くために,$[a,b]$のある開被覆$\sU$が有限部分被覆を持たないと仮定する。
- 区間を $$ \left[a,\frac{a+b}{2}\right], \ \left[\frac{a+b}{2},b\right] $$ と分割する。
- $\sU$が有限部分被覆を持たないということは,少なくともこのどちらか一方を覆う$\sU$の有限な部分集合が存在しないということである(そうでなければ,全体$[a,b]$を有限な部分集合で覆うことができてしまう)。 この有限個の開集合で覆えない区間を$[a_1,b_1]$と記す。
- $[a_1,b_1]$についても同様の分割を行い,有限個の開集合で覆えないものを$[a_2,b_2]$とする。 この操作を繰り返すことで,閉区間の集まり$\{[a_n,b_n]\ | \ n\in N \}$を作ることができる。
- これは,任意の$n$について$[a_{n+1}.b_{n+1}]\subset [a_n,b_n]$であり,$b_n-a_n=(b-a)/2^n$を満たす。
- 縮小区間定理より,すべての$[a_n,b_n]$に共通のある実数$c$が存在する。
- $\sU$は$[a,b]$の開被覆であるから,$c$を含む開集合$U$が存在する。
- このとき $$ (c-\varepsilon, c+\varepsilon) \subset U $$ となる正数$\varepsilon$が存在し,十分大きい$n$に対して $$ [a_n,b_n] \subset (c-\varepsilon, c+\varepsilon) $$ となる。
- よって,$[a_n,b_n]$は単一の開集合$U$によって被覆されることになる。
- この結論は仮定に反するから,閉区間の任意の開被覆は有限な部分被覆を持つことがわかる。
いくつかの定理
ここで,コンパクト性に関連するいくつかの定理を示す。
定理2:コンパクト空間$X$の任意の閉集合$A$はコンパクトである。
proof
- $\sU$を$X$の開集合からなる$A$の任意の被覆とする。
- $A$は$X$の閉集合であるから,$X-A$は開集合である。
- これを$\sU$に加えれば,$X$の開被覆となる。
- $X$はコンパクトであるから,$\sU$から有限部分被覆$\{U_1,U_2,...,U_k\}$を取れる。 これが$X$全体を被覆するということは,$A$も被覆する。
- $X-A$がその1つに含まれるなら,それを取り除いても$A$が被覆できるし,含まれなくとも有限個の$\{U_1,U_2,...,U_k\}$で$A$は被覆できる。
- よって,$A$はコンパクトである。
定理3:$X,Y$がともにコンパクトな位相空間なら,その積空間$X\times Y$もコンパクトになる。
proof (略)
定理4:距離空間$X$の任意のコンパクト部分集合$A$は有界である。
proof
- 任意の$x\in X$と任意の$a\in A$に対し,$d(a,x) < n$となるある整数$n$が取れる。
- すると$x$を中心とする$n$-近傍(または開球)$U_n(x)$に対し,$a\in U_n(x)$であり,$\{U_n(x) \ |\ n\in N\}$は$A$の開被覆となる。
- $A$がコンパクトであるという仮定から,有限部分被覆$\{U_{n_1},U_{n_2},...,U_{n_k}\}$を取れる。
- しかし,$\{n_1,n_2,...,n_k\}$のうち最大の整数を$N$とすると$\bigcup_{i=1}^k U_{n_i}(x)=U_N(x)$であるため,$A \subset U_N(x)$であり,$A$は有界となる。
定理5:Hausdorff空間$X$の任意のコンパクト部分集合$A$は$X$の閉集合である。
proof
$X-A$の任意の1点$x$に対し,$x \in U \subset X-A$となる開集合$U$が存在することが示せれば,$X-A$が開集合であることから,その補集合$A$が閉集合であると示せる。
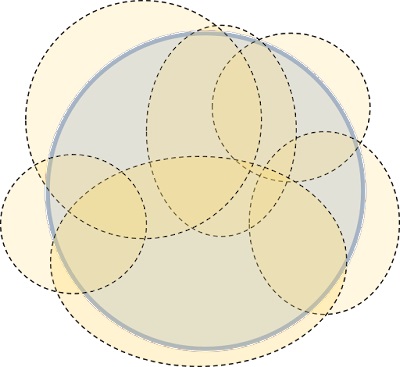
- 各$a \in A$に対し,Hausdorff条件から,$x \in U_a, a \in V_a$である互いに交わらない開集合$U_a,V_a$が存在する。
- $\{V_a | a \in A\}$は$A$の開被覆であり,コンパクト性の仮定から,有限部分被覆$\{V_{a_1},...,V_{a_k}\}$が取れる。
- $U_x=\bigcap_{i=1}^k U_{a_i}$とすると,$U_x$は開集合の共通部分であるから開集合である。
- 任意の$i$について$U_x \subset U_{a_i}$であるから,$U_x \cap V_{a_i}=\emptyset$である。
- よって
\begin{align} \notag U_x \cap A \subset U_x \cap \left(\bigcap_{i=1}^k V_{a_i}\right) = \bigcap_{i=1}^k (U_x \cap V_{a_i} ) =\emptyset \end{align}
が成り立つ。
- したがって,$U_x \subset X-A$であり,任意の$x \in X$についてこれが成り立つから,望む通りの性質が示される。

図1:定理5の証明のイメージ。$i=3$までを取った場合。
$R^n$はHausdorff空間であるから直ちに次の系が導かれる:
系1:$R^n$の任意のコンパクト部分集合は閉集合である。
Euclid空間のコンパクト部分集合
Euclid空間$R^n$に関しては次の定理が成り立つ:
定理6(Heine-Borelの定理):$R^n$の部分集合が有界閉集合であることと,コンパクトであることは同値である。
$R^n$の任意のコンパクト部分集合が有界閉集合であることは,定理4および系1からわかる。 そしてその逆が次の定理である:
定理7:$R^n$の任意の有界閉集合$A$はコンパクトである。
proof
- $n=1$の場合を考えると,$A$が有界であるということから,$A$を含む閉区間$[a,b]$が存在する。
- 定理1より,$[a,b]$はコンパクトであり,定理2よりその閉集合である$A$もコンパクトとなる。
- 一般の$n$次元の場合は,$A$は直方体$[a,b]^n$に含まれることにるが,定理3よりこの直方体もコンパクトとなる。
- よって,その閉集合である$A$はコンパクトである。
References
――(1987). 物理学における幾何学的方法. 家 正則, 観山 正見, 二間瀬 敏史 訳. 吉岡書店.