分離条件とHausdorff空間
Dr. SSS
2021/01/01 - 10:41:41
1219
位相幾何学
分離条件
($T_1$) $X$の異なる2点$x,y$に対し，$x \in U,\ y \not\in U$となる開集合$U$が存在する。
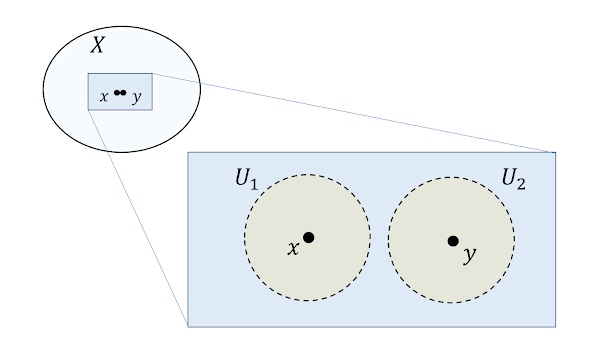
($T_2$) 異なる2点$x,y$に対し，$x \in U_1, \ y\in U_2$かつ
$$
U_1\cap U_2=\emptyset
$$
となる開集合$U_1,U_2$が存在する。
条件($T_1$)を満たすものを位相空間を$T_1$空間，条件($T_2$)を満たす位相空間を，$T_2$空間，あるいはHausdorff空間という。 物理で考察の対象となるのはまず条件($T_2$)を満たすHausdorff空間である。
参考文献
- Adams, C. and Franzosa, R. (2007). Introduction to Topology: Pure and Applied. Prentice Hall.
- 松本幸夫. (1988). 多様体の基礎. 東京大学出版会.
- Schutz, B. F. (1980). Geometrical Methods of Mathematical Physics. Cambridge University Press.
――(1987). 物理学における幾何学的方法. 家 正則, 観山 正見, 二間瀬 敏史 訳. 吉岡書店. - 志賀 浩二. (1988). 位相への30講. 朝倉書店.
- Sutherland, W. A. (2009). Introduction to Metric and Topological Spaces. Oxford University Press.
- 内田 伏一. (2020). 集合と位相(増補新装版). 裳華房.