Planckの放射式

Keywords:

リンク

Introduction

量子力学の扉を開くきっかけとなったPlanckの放射式について説明する。

黒体放射

物体は電磁波としてエネルギーを放出している。どのくらいの波長の電磁波がどれくらいの強さで放出されているかということを，熱放射のスペクトル分布という。19世紀後半の産業革命の時代，鉄製品の大量生産の需要などのため，溶鉱炉から放たれる光のスペクトルの研究が盛んになされた。スペクトル分布は物質によって異なるため，このような研究をする上でKirchhoffによって理想化された物体として黒体（black body）という概念が導入された。黒体とはあらゆる波長の電磁波を吸収する物質で，温度によってのみスペクトルが決まる。

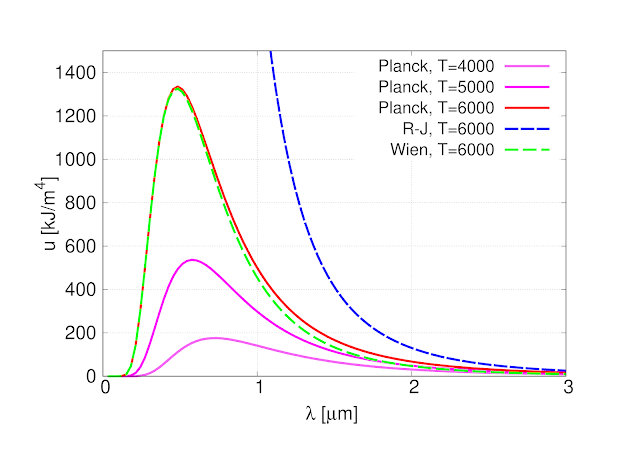
Wienは電磁気学と熱力学に基づいた考察により，（単位体積当たりの）エネルギー密度を表す式として，Wienの式（1893年）

\begin{align} u\left(\nu\right)d\nu=a\nu^3e^{-\frac{b\nu}{k_BT}}d\nu\ \end{align}

を提案した。$a,b$は定数。これは，振動数の高い領域では実験とよい一致をしたが，振動数の低い領域ではずれが大きくなった。後にRayleigh（1900年）とJeans（1905年）は，Rayleigh-Jeansの式

\begin{align} u\left(\nu,T\right)d\nu=\frac{8\pi\nu^2}{c^3}k_BTd\nu \end{align}

を導いた。これは低振動数領域では実験値をよく再現するが，高振動領域では発散する。彼らは電磁気学と統計力学(もちろん古典統計力学)を厳密に用いこの式を導いたのであるが，それでもこの黒体放射のスペクトルを正確に再現することは出来なかった。黒体放射の問題はそれまでの物理学の限界を示唆していたのである。

Planckの放射式

Planckは1900年，実験結果を再現し，結果として上の2つの式をつなぎ合わせることになる式として

\begin{align} U\left(\nu\right)d\nu=\frac{8\pi\nu^2}{c^3}\frac{h\nu}{e^\frac{h\nu}{k_BT}-1}d\nu \end{align}

を提案した。これがPlanckの放射式である。ここで

\begin{align} h=6.626\times{10}^{-34}\ {\rm J\cdot s} \end{align}

はPlanck定数と呼ばれる定数。この式は実際に振動数の大小の極限でそれぞれ

\begin{align} \frac{h\nu}{e^\frac{h\nu}{k_BT}-1} \to \left\{ \begin{array}{ll} h\nu e^{-\frac{h\nu}{k_BT}} \ &{\rm for } \ \ h\nu\gg k_BT \\ k_BT &{\rm for } \ \ h\nu \ll k_BT \end{array} \right. \end{align}

となって，（定数$a=\frac{8\pi h}{c^3},b=h$として）Wienの式と，Rayleigh-Jeansの式を再現する。

問題はこの式が意味することである。振動数$\nu$を持つ電磁波のエネルギーは，$h\nu$の整数倍

\begin{align} \varepsilon_n=nh\nu \end{align}

しかとらないと仮定すると，温度$T$で熱平衡状態にある振動子がエネルギー$\varepsilon_n$をとる確率はBoltzmann因子$e^{-\frac{\varepsilon_n}{k_BT}}$に比例し，エネルギーの平均値は

\begin{align} E=\frac{\sum_{n=0}^{\infty}{nh\nu e^{-\frac{nh\nu}{k_BT}}}}{\sum_{n=0}^{\infty}e^{-\frac{nh\nu}{k_BT}}} \end{align}

で与えられる。これは

\begin{align} \frac{\partial}{\partial\left(\frac{1}{k_BT}\right)}\ln{\left(\sum_{n=0}^{\infty}e^{-\frac{nh\nu}{k_BT}}\right)} \end{align}

と変形でき，対数の中身が初項$1$，公比$e^{-\frac{h\nu}{k_BT}}<1$の無限等比級数となっていることから

\begin{align} \frac{e^{h\nu/(k_BT)}} {e^{h\nu/(k_BT)-1}} \end{align}

に収束することを用いて

\begin{align} E=\frac{h\nu}{e^\frac{h\nu}{k_BT}-1} \end{align}

と求まる。これに状態数$8\pi\nu^2d\nu/c^3$をかけたものこそPlanckの求めた放射式に他ならない。したがって，振動子のエネルギーがとびとびの値しかとらない（これをエネルギーが量子化されているという）とすることで，黒体放射のスペクトルを説明できると言う結論に至る。この事実を当時の物理学者たちは容易に受け入れることができず，Planck自身も何とか古典論の範囲で説明できないかと試行錯誤したらしい。それでもこの結論を変えることは出来ず，後のEinsteinの光電効果に関する研究などもあり，量子論への道は拓かれていくことになる。