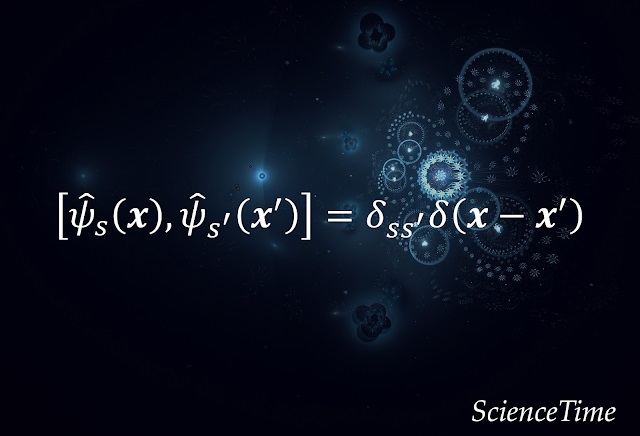はじめに
複数の同種粒子から成る系では，各粒子ごとの区別は意味を成さず，各状態を占める粒子数の数の方が重要になる。
こうした状況で有用になるのが，第二量子化と呼ばれる手法である。この記事では，ボゾンのケースに限定して，第二量子化の方法を概説する。フェルミオンのケースは別項（コチラ）で扱う。
keywords:
場の量子論,
量子力学,
生成消滅演算子,
ボゾン,
フェルミオン
内容
占有数による状態の表現
$N$個の同種粒子から成る粒子系の状態を，Dirac表記を用いて
\begin{align}
| N_1, N_2,...,N_i,...\rangle
\end{align}
と表す。
ここで$N_i$は，量子数で指定される状態のうち，$i$番目の状態を占有する粒子の数を表す。
総数はもちろん全粒子数に等しく$\sum_i N_i =N$となる。フェルミオンの場合は，排他律より$N_i$はそれぞれ$0$か$1$しかとらないが，ボゾンの場合は何個でも同じ状態を占めることができることに改めて注意しておこう。
こうして表される状態への演算を扱うため，調和振動子の項で扱った消滅演算子を一般化し
\begin{align}
\hat{a}_i| N_1, N_2,...,N_i,...\rangle
= \sqrt{N_i} | N_1, N_2,...,N_i-1,...\rangle
\end{align}
と作用する演算子$\hat{a}_i$を導入する。
同様に，Hermite共役である生成演算子$\hat{a}_i^\dagger$は
\begin{align}
\hat{a}_i^\dagger | N_1, N_2,...,N_i,...\rangle
=\sqrt{N_i+1} | N_1, N_2,...,N_i+1,...\rangle
\end{align}
と作用する。
ボゾンの場合，これらの演算子は，交換関係
\begin{align}
\hat{a}_i \hat{a}_j^\dagger -
\hat{a}_j^\dagger \hat{a}_i
=
\delta_{ij}
\end{align}
を満たす。
1粒子演算子
上述のような演算子を導入すると，$1$粒子に作用する演算子は
\begin{align}
\label {OP1}
\hat{F}^{(1)}=\sum_{i,k} \langle i |\hat{f}^{(1)} | k\rangle \hat{a}_i^\dagger \hat{a}_k
\end{align}
の形における。
ここで
\begin{align}
\langle i |\hat{f}^{(1)} | k\rangle
=
\int \psi_i^*(\xi) \hat{f}^{(1)} \psi_k (\xi) d\xi
\end{align}
である。
例えば，自由粒子の場合，Hamiltonianは
\begin{align}
\hat{h}= \frac{\hat{p}^2}{2m}
\end{align}
であるから，$i$番目の状態のエネルギー固有値を$E_i$とすれば，(\ref{OP1})の係数に対応する部分は
\begin{align}
\langle i |\hat{h}^{(1)} | k\rangle = E_k \langle i | k\rangle =E_k \delta_{ik}
\end{align}
と計算できる。
そして，(\ref{OP1})の$\hat{a}_i^\dagger \hat{a}_k$がデルタ関数と合わさって$\hat{N}_k =\hat{a}_k^\dagger \hat{a}_k $となり固有値$N_k$を与えるため，$E_k$に$k$状態を占有する粒子数がかけ合わさり，$k$状態を占める粒子の総エネルギーとして$N_k E_k $が与えられる。
全ての状態について和を取ったものが全Hamiltonian $\hat{H}^{(1)}$であるから
\begin{align}
\hat{H}^{(1)} | N_1, N_2,...,N_i,...\rangle
=\sum_i N_i E_i | N_1, N_2,...,N_i,...\rangle
\end{align}
と得られるべき結果が得られる。
2粒子演算子
1粒子の場合と同様に，2粒子に作用する演算子は
\begin{align}
\label {OP2}
\hat{F}^{(2)}=
\frac{1}{2}\sum_{i,k,l,m} \langle ik |\hat{f}^{(2)} | lm\rangle
\hat{a}_i^\dagger \hat{a}_k^\dagger \hat{a}_l \hat{a}_m
\end{align}
という形に置ける。
ここで
\begin{align}
\langle ik |\hat{f}^{(2)} | lm\rangle
=
\int \int \psi_i^*(\xi_1) \psi_k^*(\xi_2) \hat{f}^{(2)}
\psi_l (\xi_1) \psi_m(\xi_2) d\xi_1 d\xi_2
\end{align}
である。
例として，2粒子間のCoulomb相互作用を考えてみる。
簡単のためにスピン変数は省略する。
Coulombエネルギーに対応する演算子は
\begin{align}
\hat{v}^{(2)}(\bm{x}_1-\bm{x}_2)
=\frac{1}{2}\frac{\bar{e}^2}{|\bm{x}_1-\bm{x}_2|}
\end{align}
と表せる。
ここで$\bar{e}^2=e^2/(4\pi \epsilon_0)$とした。
これの行列要素は
\begin{align}
\langle ik |\hat{v}^{(2)} | lm\rangle
=&
\frac{\bar{e}^2}{2}\int \int
\frac{ \psi_i^*(\bm{x}_1) \psi_k^*(\bm{x}_2)
\psi_l (\bm{x}_1) \psi_m(\bm{x}_2)}
{|\bm{x}_1-\bm{x}_2|}
d\bm{x}_1 d\bm{x}_2
\end{align}
であるため，(\ref{OP2})に対応するのは
\begin{align}
\hat{V}^{(2)}=
\frac{\bar{e}^2}{2}
\sum_{i,k,l,m}
\left( \int \int
\frac{ \psi_i^*(\bm{x}_1) \psi_k^*(\bm{x}_2)
\psi_l (\bm{x}_1) \psi_m(\bm{x}_2)}{|\bm{x}_1-\bm{x}_2|}
d\bm{x}_1 d\bm{x}_2 \right)
\hat{a}_i^\dagger \hat{a}_k^\dagger \hat{a}_l \hat{a}_m
\end{align}
である。
そして，波動関数の直交性から，デルタ関数$\delta_{il} \delta_{km}$が与えられるため
\begin{align}
\label {vOP}
\hat{V}^{(2)}=
\frac{\bar{e}^2}{2}
\sum_{l,m}
\left( \int \int
\frac{ |\psi_l(\bm{x}_1)|^2 | \psi_m(\bm{x}_2)|^2 }{|\bm{x}_1-\bm{x}_2|}
d\bm{x}_1 d\bm{x}_2 \right)
\hat{a}_l^\dagger \hat{a}_m^\dagger \hat{a}_l \hat{a}_m
\end{align}
とできる。
係数の$1/2$は積分の重複を打ち消す（コチラを参照）。
そして
\begin{align}
\hat{\rho}_e(\bm{x})=e\sum_i |\psi_i(\bm{x})|^2 \hat{a}_i^\dagger \hat{a}_i
\end{align}
が電荷密度を与えることから，(\ref{vOP})が得られるべきCoulombエネルギーを表す演算子の形になっていることがわかる。
場の演算子
上で行われた計算は
\begin{align}
\label {fieldOP}
\hat{\psi}(\xi) = \sum_i \hat{a}_i \psi_i(\xi),
\ \
\hat{\psi}^\dagger(\xi) = \sum_i \hat{a}^\dagger_i \psi^*_i(\xi)
\end{align}
という演算子を導入することで簡潔化できることがわかる。
生成消滅演算子の性質からわかるように，$\hat{\psi}(\xi)$は，座標$\xi$に$\psi_i(\xi)$で表される粒子を生成する演算子である。
生成消滅演算子の交換関係$[\hat{a}_i, \hat{a}^\dagger_j]=\delta_{ij}$および波動関数の直交性$\sum_i \psi_i ^*(\xi) \psi_i(\xi') = \delta(\xi-\xi')$より，場の演算子の交換関係は
\begin{align}
[\hat{\psi}(\xi), \hat{\psi}^\dagger(\xi')]=\delta(\xi-\xi')
\end{align}
となる。
これらを用いると，1粒子および2粒子に対する演算子はそれぞれ
\begin{align}
\hat{F}^{(1)}
=\int \hat{\psi}^\dagger(\xi ) \hat{f}^{(1)} \hat{\psi}(\xi) d\xi
\end{align}
および
\begin{align}
\hat{F}^{(2)}
=\frac{1}{2}\int
\hat{\psi}^\dagger(\xi )\hat{\psi}^\dagger(\xi' )
\hat{f}^{(2)} \hat{\psi}(\xi')\hat{\psi}(\xi) d\xi d\xi'
\end{align}
と表される。
また，波動関数の正規直交性$\int \psi^* \psi d\xi=1$より
\begin{align}
\int \hat{\psi}^\dagger(\xi)\hat{\psi}(\xi) d\xi
=
\sum_i \hat{a}_i^\dagger \hat{a}_i
=\hat{N}_i
\end{align}
の関係も成り立つ。
(\ref{fieldOP})の導入は，電磁場の量子化において，場を固有関数で展開し，その係数を生成消滅演算子と置くことで演算子化したのと同様の手続きである。
このように，波動関数を古典場と同様の手続きによって演算子化することを第二量子化という。
しかし，第二量子化は古典論から量子論への移行のような枠組みの変化を生じるものではないから，現在ではこの呼び方は不適切か，あるいは注意が必要なものとみなされている。
