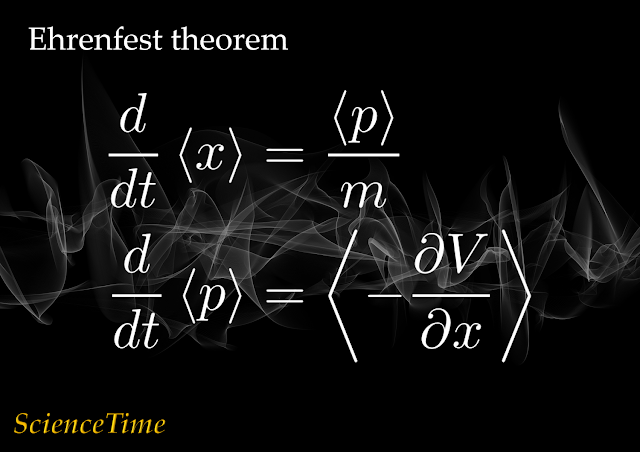リンク
Introduction
ここでは,位置と運動量の期待値の時間変化を記述し,古典力学と量子力学の橋渡しをするEhrenfestの定理と呼ばれる関係
\begin{align}
\frac{d}{dt}\left\langle x\right\rangle
&=\frac{\left\langle p\right\rangle}{m} \\
%
\frac{d}{dt}\left\langle p\right\rangle
&=\left\langle-\frac{\partial V}{\partial x}\right\rangle
\end{align}
を導く。
導出
位置の期待値の時間微分は,定義の通り
\begin{equation}
\begin{split}
\frac{d}{dt}
\left\langle x \right\rangle
&=
\frac{d}{dt}
\int_{-\infty}^{\infty}
\psi^*\hat{x}\psi dx \\
&=
\int_{-\infty}^{\infty}
\frac{\partial\psi^*}{\partial t}
\hat{x}\psi dx
+
\int_{-\infty}^{\infty}
\psi^*\hat{x}
\frac{\partial\psi}{\partial t}dx
\end{split}
\end{equation}
となる。これをSchrödinger方程式およびその複素共役
\begin{equation}
i\hbar\frac{\partial\psi}{\partial t}
=\hat{H}\psi,
\quad
-i\hbar\frac{\partial\psi^*}{\partial t}
=\hat{H}\psi^*
\end{equation}
を用いて
\begin{equation}
\begin{split}
\frac{d}{dt}\left\langle x\right\rangle
&=\int_{-\infty}^{\infty}
\left[\left(-\frac{1}{i\hbar}\hat{H}^*\psi^* \right)\hat{x}\psi
+\psi^*\hat{x}
\left(\frac{1}{i\hbar}\hat{H}\psi\right)\right]dx \\
%
&=\frac{i}{\hbar}
\int_{-\infty}^{\infty}
\left(\psi^*\hat{H}\hat{x}\psi-\psi^*\hat{x}\hat{H}\psi\right)dx \\
%
&=\frac{i}{\hbar}\int_{-\infty}^{\infty}\psi^*\left[\hat{H},\hat{x}\right]\psi dx
\end{split}
\end{equation}
と変形する。 ここで,Hamiltonianと位置演算子の交換関係は
\begin{equation}
\begin{split}
\left[\hat{H},\hat{x}\right]
&=\left[\frac{\hat{p}^2}{2m}+V,\hat{x}\right]
=\frac{1}{2m}\left[{\hat{p}}^2,\hat{x}\right]
=\frac{1}{2m}\left(\hat{p}\left[\hat{p},\hat{x}\right]
+\left[\hat{p},\hat{x}\right]\hat{p}\right) \\
&=-\frac{i\hbar}{m}\hat{p}
\end{split}
\end{equation}
となるため位置の期待値の時間微分は
\begin{equation}
\frac{d}{dt}\left\langle x\right\rangle
=\frac{i}{\hbar}
\int_{-\infty}^{\infty}\psi^*\left[\hat{H},\hat{x}\right]\psi dx
=\frac{\left\langle p\right\rangle}{m}
\end{equation}
となることがわかる。
次に,運動量$p$の期待値の時間微分を考える。この場合も位置の期待値の場合と同様
\begin{equation}
\begin{split}
\frac{d}{dt}\left\langle p\right\rangle
&=\frac{d}{dt}\int_{-\infty}^{\infty}{\psi^\ast\hat{p}\psi dx} \\
&=\int_{-\infty}^{\infty}
\frac{\partial\psi^*}{\partial t}\hat{p}\psi dx
+\int_{-\infty}^{\infty}
\psi^\ast\hat{p}\frac{\partial\psi}{\partial t}dx \\
&=\frac{i}{\hbar}\int_{-\infty}^{\infty}\psi^\ast\left[\hat{H},\hat{p}\right]\psi dx
\end{split}
\end{equation}
となる。Hamiltonianと運動量の交換関係は
\begin{equation}
\begin{split}
\left[\hat{H},\hat{p}\right]
&=
\left[\frac{{\hat{p}}^2}{2m}+V,\hat{p}\right] \\
&=V\left(-i\hbar\frac{\partial}{\partial x}\right)
-\left(-i\hbar\frac{\partial}{\partial x}V\right) \\
&=i\hbar\frac{\partial}{\partial x}V
\end{split}
\end{equation}
と計算されるため,運動量の期待値の時間微分は
\begin{equation}
\frac{d}{dt}\left\langle p\right\rangle
=\left\langle-\frac{\partial V}{\partial x}\right\rangle
\end{equation}
となる。
古典力学との対応と注意
これらの結果は,3次元の場合
\begin{equation}
\begin{split}
\frac{d\ev{\bm{x}}}{dt}
=&\frac{\ev{\bm{p}}}{m} \\
%
\frac{d\ev{\bm{p}}}{dt}
=&
-\ev{\nabla V}
=\ev{\bm{F}}
\end{split}
\end{equation}
となり,それぞれ古典力学の運動方程式
\begin{equation}
\begin{split}
\frac{d\bm{x}}{dt}
=&\frac{\bm{p}}{m} \\
\frac{d\bm{p}}{dt}
=&-\nabla V
=\bm{F}
\end{split}
\end{equation}
に対応している。
ただし,この対応について一つ注意が必要である。 点$\ev{\bm{x}}$というのは,期待値として得られる一点である。 古典的な運動方程式のように,ちょうどその点ある粒子の運動が,その点における力$\bm{F}(\ev{\bm{x}})$の値で決まるような描像が成り立つのは,力の期待値
\begin{equation}
\ev{\bm{F}}
=
\int_{-\infty}^\infty
\psi^* (-\nabla V)\psi d^3x
\end{equation}
が,点$\ev{\bm{x}}$での力の値$\bm{F}(\ev{\bm{x}})$と十分近い必要がある。 一般にそれが成り立つのは,波束が$\ev{\bm{x}}$の周辺に局在しているような場合である(その他それが成り立つ特殊な例についてはMessiah (2014)を参照)。 Ehrenfestの定理は,そのような条件の下では,波束は古典論的粒子のように振る舞うのだということを示している。
References
—(1971). メシア量子力学. 小出昭一郎&田村二郎 訳. 東京図書
―(1970). 量子力学. 井上健 訳. 吉岡書店.