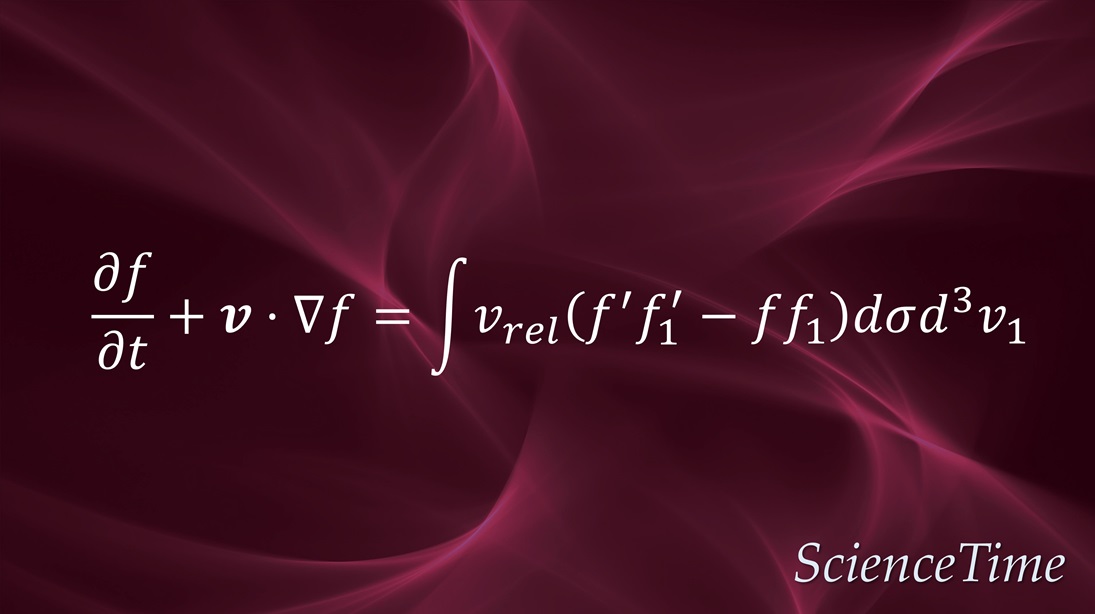Boltzmann方程式

分子間距離

一様に分布する粒子の数密度（単位体積中の粒子数）は，全粒子数$N$を全体積$V$で割り

と与えられる。 これに，ある領域の体積$\Delta V$をかければ，$\Delta V$中にある粒子数$\Delta N$が得られる：

この考えを用いると，一様な気体中の分子間の距離$\overline{r}$が見積もれる。 分子1つが占める体積は$\sim\overline{r}^3$であるから，密度$n$にこれをかけたものは，$\sim1$となるはずである。 よって$n\overline{r}^3 \sim 1$，すなわち

である。

以下，理想的で十分希薄な気体を考え，このパラメータが分子間力が作用する距離スケール$d$より十分大きいこと

を仮定する。 そしてこれより，衝突による分布関数の変化に関して，2粒子間の衝突のみを考慮し，3粒子以上の粒子が関与する衝突の影響は無視できることとする。

衝突の回数

ある点$\bm{x}$における2粒子間の衝突を考える。 一方の粒子は，速度空間内で$\bm{v}$から幅$d\bm{v}$の中にあるものとし，もう一方の粒子は$\bm{v}_1$から幅$d\bm{v}_1$の中にあるものとする。 そして，これらの粒子は衝突により，それぞれ$\bm{v}'$および$\bm{v}_1'$に変化するとする。

このような衝突が起きる頻度は，単位体積あたり単位時間内に衝突に参加する粒子数に対応する量$f(t,\bm{x},\bm{v})d\bm{v}$と$f(t,\bm{x},\bm{v}_1)d\bm{v}_1$，そして散乱先の速度領域の大きさ$\bm{v}'+d\bm{v}'$と$\bm{v}_1'+d\bm{v}_1'$に比例するはずである。 よって，単位体積あたり単位時間内に起こる，$\bm{v},\bm{v}_1$から$\bm{v}',\bm{v}_1'$への衝突散乱の数は

となる。 ここで関数$w$の引数は，衝突前の変数を右に，衝突後の変数を左に記すこととする。

速度$\bm{v}$の粒子が単位時間内で単位体積中に起こす衝突の総数は，$w(\bm{v}',\bm{v}_1';\bm{v},\bm{v}_1)f(t,\bm{x},\bm{v})f(t,\bm{x},\bm{v}_1)$を，衝突後の速度$\bm{v}',\bm{v}_1'$と，衝突相手の速度$\bm{v}_1$について積分すれば得られる。 これは速度空間$\bm{v}$から出ていく粒子の数であるから，$(\pd f/\pd t)_{coll}$のうち，減少分に対応する：

ここで，$w=w(\bm{v}',\bm{v}_1';\bm{v},\bm{v}_1)$，$f=f(t,\bm{x},\bm{v})$および$f_1=f(t,\bm{x},\bm{v}_1)$と略記した。

他方，衝突により，速度空間$\bm{v}$に入ってくる粒子もある。 この寄与は

で与えられる。 ここでも，$w'=w(\bm{v},\bm{v}_1;\bm{v}',\bm{v}_1')$，$f'=f(t,\bm{x},\bm{v}')$および$f_1'=f(t,\bm{x},\bm{v}_1')$と記した。

衝突による分布関数の正味の変化は(\ref{eq:collision_term_in})から(\ref{eq:collision_term_out})を差し引いて

と得られる。

詳細釣り合いの原理

ところで，運動方程式の時間反転対称性より，$\bm{v},\bm{v}_1$から$\bm{v}',\bm{v}_1'$への衝突に対し，速度を反転させた$-\bm{v}',-\bm{v}_1'$から$-\bm{v},-\bm{v}_1$への衝突も同じ頻度で起こる（$d\bm{x}/(-dt)=-d\bm{x}/dt$）。 したがって

である。 これを，詳細釣り合いの原理（principle of detailed balance）と呼ぶ。

時間反転に対してだけでなく，系が等方的であれば，空間反転に対しても対称性を持つ（$d(-\bm{x})/dt=-d\bm{x}/dt$）。 それゆえ

Boltzmann方程式

(\ref{eq:w_time_reversal})および(\ref{eq:w_spatial_inversion})より結局

が成り立つ。 その結果，衝突項は

となる。 これを，Boltzmann衝突項（Boltzmann collision term）やBoltzmann衝突積分（Boltzmann collision integral）と呼ぶ。 そして，Boltzmann衝突項を右辺に持つ

を，Boltzmann方程式（Boltzmann equation）と呼ぶ。

ところで，$w$は$\mathrm{[L^{-3}T^5]}$の次元を持っている。 よって

は面積の次元を持っており，有効衝突断面積を表す。 ここで，$v_{rel}=|\bm{v}-\bm{v}_1|$とした。 これを用いるとBoltzmann衝突項は

と表すこともできる。

改めて，系の数密度が十分小さいということから，Boltzmann衝突項には，2体衝突の影響のみが含まれている。 また，衝突が起こる見込みが分布関数の単純な積で与えられているということは，どの時刻においても，衝突粒子のペアは衝突前に相関を持たないという仮定に基づいている。 これら2つの仮定を合わせて，分子混沌（Stosszahlansatz, molecular chaos）と呼ばれる。